Ламінарний плин рідини у вузьких щілинах

Вище був розглянутий найбільш простий випадок ламінарного режиму – рівномірний рух рідини в круглій трубі. Однак у техніці мають місце і більш складні випадки, до числа яких відноситься ламінарний рух у плоских і кільцевим.

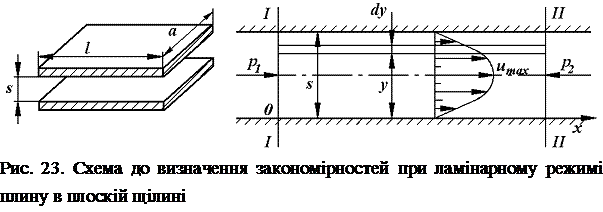
Розглянемо рівномірний ламінарний рух рідини в плоскій щілині (зазорі між двома пластинками) довжиною 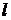 шириною  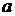і висотою  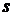            (рис. 23). Позначимо різницю тисків на вході і виході з щілини .

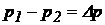Застосовуючи той же метод, що був використаний для висновку рівняння 81, можна одержати рівняння для визначення швидкості в будь-якій крапці щілини по вертикалі

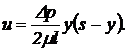                                                                                  (85)

Максимальна швидкість буде при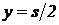

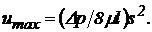                                                                             (86)

Для визначення витрати рідини необхідно обчислити інтеграл

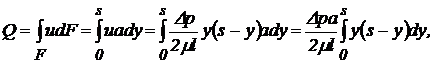                 (87)

відкіля витрата рідини через щілину (витік через зазор)

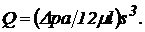                                                                              (88)

Середня швидкість потоку може бути отримана як частка від розподілу витрати Q на живий перетин (площа щілини) 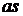, тобто

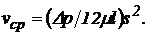                                                                              (89)

Таким чином, відношення середньої швидкості до максимальної для плоскої щілини .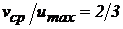

Отримані формули можуть бути використані також і для концентричних кільцевих щілин (наприклад, щілин, утворених співвісними плунжером діаметром 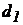 і циліндром діаметром 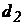). якщо висота щілини (величина зазору між плунжером і циліндром)  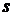значно менше діаметра плунжера, тобто 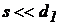. Для визначення витрати (витоку) рідини через щілину в цьому випадку в рівняння (88) замість  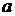варто підставляти .

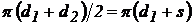У випадку ексцентричної кільцевої щілини в (88) замість 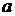 варто підставляти 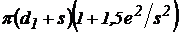, де 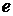 – ексцентриситет між осями плунжера і циліндра.