З вираження (84) можна, знаючи середню швидкість рідини при ламінарному режимі плину в трубі, можна знайти втрату тиску на тертя на ділянці 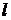
 .
.
Питома втрата тиску на подолання тертя (віднесена до одиниці сили ваги 1 кг рідини)
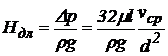 чи
чи  . (91)
. (91)
Отримане рівняння виражає закон гідравлічного опору при ламінарному режимі руху рідини. Це вираження зветься формулою Пуазейля, французького лікаря і фізика.
Перетворимо (91), помноживши чисельник і знаменник на 
 (92)
(92)
Порівнюючи дане вираження з (78), одержимо коефіцієнт Дарсі 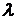 для круглої труби
для круглої труби
 (93)
(93)
Однак експериментальні дослідження, проведені в останні роки, показують, що фактичне значення 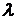 може відрізнятися від теоретичного, обумовленого з (93). У загальному випадку
може відрізнятися від теоретичного, обумовленого з (93). У загальному випадку  , де
, де 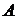 може мати значення
може мати значення  . Для мастилопроводів гідроприводів приймають
. Для мастилопроводів гідроприводів приймають  .
.
Формула (92) має ім'я Дарсі-Вейсбаха, чи називається I водопровідною формулою і виражає втрати напору в трубі у функції середньої швидкості рідини, що протікає.
Оскільки  , де
, де 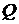 – витрата рідини, то
– витрата рідини, то
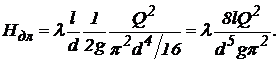 (94)
(94)
Ця формула називається II водопровідною формулою і виражає втрати напору у функції витрати рідини в трубі.
Звертаємо увагу на те, що хоча для розрахунку втрат при ламінарному плині користуються, в основному, формулами (92) і (94), куди входить швидкість (чи витрата) у другому ступені, у дійсності втрати напору пропорційні швидкості (чи витраті) у першому ступені, як це випливає з формули (91) Пуазейля. Справді, коефіцієнт 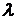 у формулах (92) і (94) містить у знаменнику величину
у формулах (92) і (94) містить у знаменнику величину  , а виходить, і швидкість. Після скорочення виходить швидкість у першому ступені.
, а виходить, і швидкість. Після скорочення виходить швидкість у першому ступені.
Отже, втрати напору при ламінарному плині є лінійною функцією швидкості (чи витрати) рідини.
Втрати напору при турбулентному плині обчислюють також по формулі Дарсі-Вейсбаха, але коефіцієнт утрат на тертя 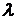 визначають не формулою (93).
визначають не формулою (93).
Велике значення для визначення втрат на тертя при турбулентному плині має поняття шорсткості. Внутрішня поверхня труб (і будь-яких інших магістралей для плину рідини) має мікро нерівності, абсолютну величину яких  називають абсолютною шорсткістю, а її відношення до діаметра
називають абсолютною шорсткістю, а її відношення до діаметра  – відносною шорсткістю. Так, наприклад, абсолютна шорсткість для деяких видів труб така: сталеві безшовні труби нові і чисті –
– відносною шорсткістю. Так, наприклад, абсолютна шорсткість для деяких видів труб така: сталеві безшовні труби нові і чисті –  , сталеві безшовні труби після декількох років експлуатації –
, сталеві безшовні труби після декількох років експлуатації –  , нові сталеві зварні труби –
, нові сталеві зварні труби –  , сталеві зварені труби помірковано заржавлені –
, сталеві зварені труби помірковано заржавлені – 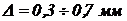 , нові чавунні труби –
, нові чавунні труби –  , чавунні труби колишні у вживанні –
, чавунні труби колишні у вживанні –  , рукави і шланги –
, рукави і шланги –  .
.
Якщо товщина ламінарного підшару покриває нерівності ( ), труби називають гідравлічно гладкими, у противної випадку – гідравлічно шорсткуватими. Та сама труба може бути гідравлічно гладкою чи шорсткуватою у залежності від товщини
), труби називають гідравлічно гладкими, у противної випадку – гідравлічно шорсткуватими. Та сама труба може бути гідравлічно гладкою чи шорсткуватою у залежності від товщини  , а виходить, від швидкості потоку.
, а виходить, від швидкості потоку.
Коефіцієнт втрат при турбулентному плині залежить, в основному, від двох параметрів – числа Рейнольдса  і відносної шорсткості
і відносної шорсткості  . Вплив цих параметрів на коефіцієнт втрат вивчали багато дослідників, з яких особливо слід зазначити І.І.Нікурадзе і Г.А.Муріна. І.І.Нікурадзе досліджував плин рідини в трубах зі штучно створеною “рівномірною” шорсткістю в широкому діапазоні шорсткостей
. Вплив цих параметрів на коефіцієнт втрат вивчали багато дослідників, з яких особливо слід зазначити І.І.Нікурадзе і Г.А.Муріна. І.І.Нікурадзе досліджував плин рідини в трубах зі штучно створеною “рівномірною” шорсткістю в широкому діапазоні шорсткостей 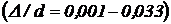 і чисел Рейнольдса (
і чисел Рейнольдса ( ), Г.А.Мурін – у працях із природною, “нерівномірною” шорсткістю. Результати дослідів І.І.Нікурадзе показані на графіках рис. 25, побудованих у логарифмічних координатах.
), Г.А.Мурін – у працях із природною, “нерівномірною” шорсткістю. Результати дослідів І.І.Нікурадзе показані на графіках рис. 25, побудованих у логарифмічних координатах.

При ламінарному плині зв'язок між  і
і  визначається залежністю
визначається залежністю  (графік – пряма I). При турбулентному плині і гідравлічно гладких трубах зв'язок між
(графік – пряма I). При турбулентному плині і гідравлічно гладких трубах зв'язок між  і
і  визначається
визначається
при  формулою Блазіуса (графік – пряма II):
формулою Блазіуса (графік – пряма II):
 (95)
(95)
При  зручна формула П. К. Конакова:
зручна формула П. К. Конакова:
 (96)
(96)
У зоні III коефіцієнт  залежить як від числа Рейнольдса, так і від відносної шорсткості.
залежить як від числа Рейнольдса, так і від відносної шорсткості.
При турбулентному плині і гідравлічно шорсткуватих трубах (зона IV) коефіцієнт утрат  перестає залежати від числа
перестає залежати від числа  , а є функцією тільки відносної шорсткості (так називана автомодельна зона) і може бути підрахований по формулі Нікурадзе-Прандтля
, а є функцією тільки відносної шорсткості (так називана автомодельна зона) і може бути підрахований по формулі Нікурадзе-Прандтля
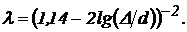 (97)
(97)
Для визначення  у всій області турбулентного плину (для зон II, III і IV) може бути використана універсальна формула Альтшуля
у всій області турбулентного плину (для зон II, III і IV) може бути використана універсальна формула Альтшуля
 (98)
(98)
Графіки, отримані Г.А.Муріним для труб із природною шорсткістю, відрізняються від графіків І.І.Нікурадзе тим, що в III зоні на них відсутні западини, тобто похила пряма ділянка плавно переходить у прямі горизонтальні ділянки IV зони.
Оскільки для IV зони  не залежить від
не залежить від  формула (97), з формули Дарсі-Вейсбаха (92) випливає, що втрати на тертя залежать від квадрата швидкості, тобто має місце квадратичний закон опору. Для II і III зон показник ступеня швидкості (у вираженні втрат) поступово зростає від
формула (97), з формули Дарсі-Вейсбаха (92) випливає, що втрати на тертя залежать від квадрата швидкості, тобто має місце квадратичний закон опору. Для II і III зон показник ступеня швидкості (у вираженні втрат) поступово зростає від 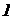 до
до 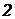 .
.
 2018-02-14
2018-02-14 485
485








