Определение обобщенной силы

 

Обобщенная сила вычисляется как частное от деления мощности всех сил, действующих на систему, на обобщенную скорость.

                              ;                                       Мощность сил, действующих на систему, вычисляется для сил тяже-

сти элементов пантографа и сил упругости  двух пружин:

;

    Мощность указанных сил определяем как скалярное произведение вектора силы на вектор скорости точки ее приложения:

                      

В том случае, когда сила приложена к вращающемуся элементу, удобно определять мощность по произведению момента силы относительно оси вращения элемента на угловую скорость его вращения:

    В нашем случае:

 

;

 

;

 

;

 

;

 

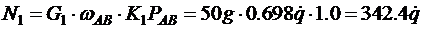    Мощность силы упругости половины пружины:

Здесь величина силы упругости, определяемая как произведение коэффициента жесткости пружины  и полной деформации пружины, которая складывается из рабочего хода 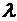 и статической деформации . Рабочий ход пружины (перемещение точки )  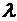выражается через обобщенную координату также как скорость точки  через обобщенную скорость: .

Следует учесть, что растяжение пружины на величину 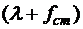 происходит и с одним и с другим ее концом т.е. полная мощность силы упругости пружины

.

В результате суммарная мощность принимает вид:

 

;

 

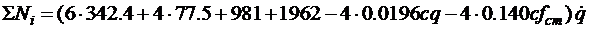или .

То есть .

 

Величину статической деформации пружины  определяем из условия равновесия: . В нашем случае  , откуда ,

 

Подставив полученное выражение в формулу для ,  получим:

                 .

Здесь  коэффициент жесткости системы.

 

 

Определение частоты свободных колебаний

Пантографа.

 

Подставляем полученные выражения кинетической энергии и обобщенной силы в уравнение Лагранжа II рода:

;

После выполнения необходимых операций получим дифференциальное уравнение свободных колебаний:

; или

.

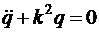Здесь  циклическая частота свободных колебаний.

В нашем случае .

 

Период полного колебания составляет:

 

 

Определение частот вынужденных колебаний

Пантографа.

 

Скорость движения электропоезда меняется от 0 до 120 км/ч. Колебания, вызванные перемещениями токосъемника вместе с контактным проводом во время движения, являются вынужденными колебаниями пантографа. Контактный провод можно считать провисающим по синусоиде с вершинами у опор контактной сети. Таким образом, период вынужденных колебаний соответствует времени прохождения составом расстояния между опорами. Приняв расстояние равным  получим граничные значения периода и частоты вынужденных колебаний:

;

    Этому периоду соответствует частота

 

,

т.е. частота вынужденных колебаний может меняться от 0 до .