Дифференциальные уравнения равновесия жидкости

Основное уравнение гидростатики становится неприемлемым в случае, когда кроме силы тяжести действуют и другие массовые силы (сила инерции, центробежная сила и др.).

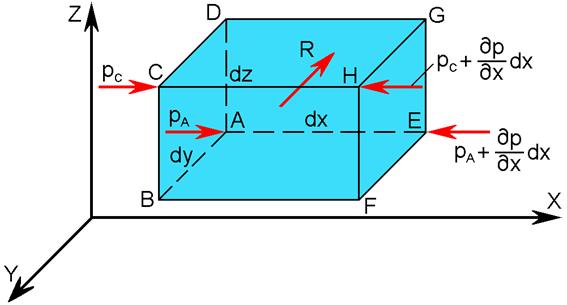
Рис.2.8.Схема для вывода дифференциальных уравнений

равновесия жидкости

Для получения более общего решения выведем дифференциальные уравнения равновесия жидкости.

В сосуде с неподвижной относительно него жидкостью возьмем произвольный объем жидкости в виде параллелепипеда с ребрами dx, dy, dz (рис.2.8). Отбросив окружающую параллелепипед жидкость, необходимо заменить ее действие силами. Это будут сжимающие поверхностные силы давления. Кроме поверхностных сил на жидкость в объеме параллелепипеда действуют массовые силы. Равнодействующая массовых сил равна DRDW, плотность распределения которой R.

Проекции R на оси координат обозначим, соответственно, R_x, R_y и R_z. Пусть от действия поверхностной силы на грань АВСD давление в точке А составит р_А. На рис.2.8. оно показано действующим вдоль ребра АЕ. Очевидно, что вдоль ребер АВ и АD действует такое же давление. Это вытекает из свойства гидростатического давления. Вместе с тем, давление р является функцией координат х, у и z.

При переходе от точки А, например, к точке Е, изменяется лишь координата х на бесконечно малую величину dх. В этой связи функция р получает приращение, равное частному дифференциалу . Тогда давление в точке Е составит р_А + . Здесь является градиентом давления вблизи точки А в направлении оси х.

Рассматривая давления в других соответствующих точках граней, перпендикулярных к оси х, например, С и Н, видно, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину

.                     (2.14)

Тогда уравнение равновесия параллелепипеда в направлении оси х запишется в виде

.                    (2.15)

В этой формуле dxdydz = DW - объем параллелепипеда,
а dydz = DS - площадь грани параллелепипеда, нормальная к оси х.

Разделив все члены этого уравнения на массу жидкости параллеле­пипеда DM = Ddxdydz, получим

.                              (2.16)

Поступая аналогично в направлении осей ОУ и 0Z, получим окончательно

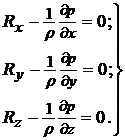,                           (2.17)

Данная система дифференциальных уравнений гидростатики называется уравнениями Эйлера.

На практике удобнее пользоваться вместо системы уравнений (2.17) одним эквивалентным уравнением, не содержащим частных производных.

Для этого умножим первое уравнение на dx, второе - на dу, третье - на dz и просуммируем все три уравнения

.   (2.18)

Выражение в скобках представляет собой полный дифференциал давления, поэтому можем переписать предыдущее уравнение в виде  или

.               (2.19)

Полученное уравнение выражает приращение давления dр при изменении координат на dх, dу, dz в общем случае относительного покоя жидкости.

Поверхности уровня (поверхности равного давления) из условия dр = 0 при описываются дифференциальным уравнением вида

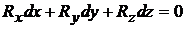.                         (2.20)