

1)проверяем 1-е условие для переходной матрицы: 
(да, условие выполняется)
2)граничное условие 
Воспользуемся аппаратом линейной алгебры. Рассмотрим простой случай, когда матрица А является диагональной.



Приведем А к диагональному виду.  ;
; 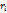 -собственный вектор соответствующего собственного значения
-собственный вектор соответствующего собственного значения 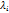 .
.
Из столбцов составим матрицу векторов: 


 (преобразование подобия)
(преобразование подобия)
Справедливо для целых степеней - 
3.2) 
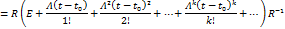

Алгоритм:
1)Отыскиваются собственные значения матрицы  (корни хар-го выражения)
(корни хар-го выражения) 
2)Отыскиваем собственные вектора по выражению 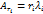 . Строим матрицу
. Строим матрицу 
3)Подставляем в 


Условия управляемости и наблюдаемости Гильберта для систем, состоящих из подсистем.
 111 111
|
  4 5 6 7 8 13 17 18 19 22 33 34 35 36 37 44 45 4 5 6 7 8 13 17 18 19 22 33 34 35 36 37 44 45
|

|

|
 - полностью управляема и наблюдаема;
- полностью управляема и наблюдаема;  – управляема, но не наблюдаема;
– управляема, но не наблюдаема;  - не управляема и ненаблюдаема;
- не управляема и ненаблюдаема;  – не управляема, но наблюдаема.
– не управляема, но наблюдаема.
Условие Гилберта может исследовать соединения: последовательные, параллельные и с обратной связью.
Последовательное соединение.
 :
: 
 :
: 

Необходимым условием наблюдаемости  является наблюдаемость каждой подсистемы, т.е.
является наблюдаемость каждой подсистемы, т.е.  и
и  . Если
. Если  и
и  полностью наблюдаемы, а
полностью наблюдаемы, а  не является наблюдаемой, то ее наблюдаемое решение принадлежит
не является наблюдаемой, то ее наблюдаемое решение принадлежит  . Необходимое условие управляемости
. Необходимое условие управляемости  является управляемость
является управляемость  и
и  . Если
. Если  не управляема, то неуправляемое движение принадлежит
не управляема, то неуправляемое движение принадлежит  .
.
Параллельное соединение.
Описание  :
: 


Условие наблюдаемости и управляемости всей системы заключается в наблюдаемости и управляемости каждой подсистемы.
С обратной связью.

|

|


 Необходимым и достаточным условием наблюдаемости замкнутой системы
Необходимым и достаточным условием наблюдаемости замкнутой системы  является наблюдаемость вспомогательной системы
является наблюдаемость вспомогательной системы  в виде последовательного соединения. Если
в виде последовательного соединения. Если  и
и  полностью наблюдаемы, то ненаблюдаемое движение S является ненаблюдаемым движением
полностью наблюдаемы, то ненаблюдаемое движение S является ненаблюдаемым движением  и порождается подсистемой
и порождается подсистемой  .
.
7.1) Рассмотрим SISO (1 вх и 1 вых), цель – придать замкнутой системе желаемый вид.
u(t)=g(t)-v(t)
G=[g1,g2,…,gn]
v(t)=g1x1(t)+ g2x2(t)+…+ gnxn(t)
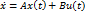 , разомкнутая система g(t)=0 (в свободной системе)
, разомкнутая система g(t)=0 (в свободной системе)
Замыкание: 

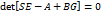 (1)
(1)
Пусть желаемое расположение корней, тогда
(S-λ1) (S-λ2)… (S-λn)=0 (2)
 Раскрываем определитель (1), раскрывается (2) и получаем n штук алгебр урав-ий, приравнивая коэф-ты при одинаковых степенях s в (1) и (2). Из (1) n-штук неизвестных коэфф-ов, которые дают n штук ур-ий и из этой сис-мы находим коэфф-ты gi.
Раскрываем определитель (1), раскрывается (2) и получаем n штук алгебр урав-ий, приравнивая коэф-ты при одинаковых степенях s в (1) и (2). Из (1) n-штук неизвестных коэфф-ов, которые дают n штук ур-ий и из этой сис-мы находим коэфф-ты gi.

 При завышенных требованиях коэффициенты м.б. очень большими, т.е. область линейности (огран.), не позволит реализоваться сигналам (v(t)), т.е. нужен огромный сигнал на выходе, что нереализуемо на практике. Также нужно иметь информацию о вект. сост. x(t), а это нереально (нужно иметь n датчиков);
При завышенных требованиях коэффициенты м.б. очень большими, т.е. область линейности (огран.), не позволит реализоваться сигналам (v(t)), т.е. нужен огромный сигнал на выходе, что нереализуемо на практике. Также нужно иметь информацию о вект. сост. x(t), а это нереально (нужно иметь n датчиков);
7.2) Строят след. систему с помощью наблюдателя (устр-во, основ-ое на построении модели объекта управления)
Задача: по вх. воздействию и измеряя вых. сигнал восст. вект. сост.
 – оценка вект. сост-я (с погрешностями и с задержкой, если устройство цифровое)
– оценка вект. сост-я (с погрешностями и с задержкой, если устройство цифровое)
Желаемое распределение корней в модальном управлении.
1.Биномиальное распределение.
D(s)=(s+ω0)n ;Все корни в одной точке, быстродействие нелучшее.

2.Баттерворта
Располаг. корни на окружности радиуса ω0
Быстродействие лучше, более высокое, но при наличии выброса.
3.Расположение, полученное в рез-те минимизации по критерию квадрата ошибки.
7.3) 
ПП быстрее, но выбросы больше, лучшее быстродействие в лин. сис-ме.
4. 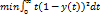
 Метод дает высокое быстродействие с ограничением выброса (чуть хуже по времени чем 3., но σ существенно меньше.)
Метод дает высокое быстродействие с ограничением выброса (чуть хуже по времени чем 3., но σ существенно меньше.)
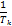
|
 2018-02-14
2018-02-14 270
270








