Метод гармонического баланса

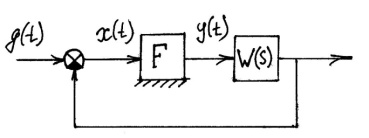
сигналы g(t) и выход сист. знач. не имеют. g(t)=0

Безинерц-ая нелин-ть(которая симметрична относ. начала координат)отделена от динамич лин-й части.

Предположим, что в этой системе найдется переодич-ое решение: будем считать, что на входе линейного элемента сигнал x(t), на выходе y(t). Сигнал g(t) и выход значения не имеют.

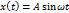 тогда на выходе: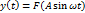

Пользуемся методом гармон-й линеаризации нелин-ти. Сигнал на выходе y(t) мы заменяем 1-й гармоникой: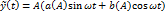

Передаточная функция линейной части д.б. фильтром низких частот. Вводится погрешность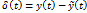

Идет линеаризация:

 

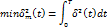
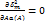
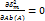
17.2)

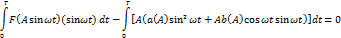
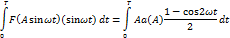
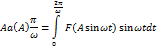
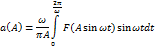
Аналогично получаем:

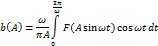
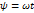 - перешли к другой переменной

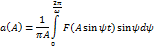
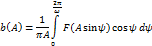
Преобразование сигнала, проходящего через нелин. Элемент.

17.3)

Для однозначной нелинейности:

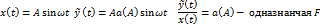
Для 2-хзначной нелинейности:

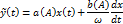
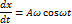
Вывод: становится важно, растет или убывает сигнал.

В результате гармонической линеаризации не теряем свойства, присущее линейным элементам.

Коэффициент гармонической линеаризации не зависит от частоты(при нашей постановке задачи)

Введем понятие эквивалентного гармонически линеаризованного коэффициента усиления

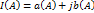
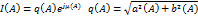
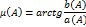
Фаза сдвигается, кода есть косинусная составляющая b(A)