Решение линейной нестационарной системы в пространстве состояний

Переходная матрица. Методы ее нахождения и ее свойства.

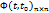 – переходная матрица, матрица перехода из одного состояния в другое.

Она должна удовлетворять решению однородной системы:

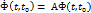
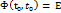
Для нестационарной системы:

t1>t0:    x(t1)=Ф(t1,t0)*x(t0)

t2>t1:    x(t2)=Ф(t2,t0)*x(t0)

                   x(t2)= Ф(t2,t1)*x(t1)= Ф(t2,t1)* Ф(t1,t0)*x(t0) => Ф(t2,t0)= Ф(t2,t1)* Ф(t1,t0) =>

=> Ф(t,t0)* Ф(t0,t) = Ф(t0,t)* Ф(t,t0)=E

Для вычисления обратной матрицы, нужно поменять местами аргументы: Ф^-1(t,t0)=Ф(t0,t)

Для стационарной системы:

Ф(t,t0)= +… (*)

Проверим условия 1) и 2)

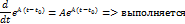
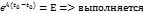
Рассмотрим простейший случай, когда матрица A является диагональной

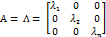
Ф(t,t0) =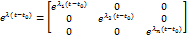

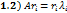 , где 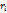 - собственный вектор, соответствующий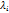

Составим из векторов блочную матрицу R

R =  ,  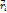– вектор-столбец

AR=RΛ, Λ – диагональная матрица

А=RΛR^-1

Λ=R^-1AR, это справедливо для целых степеней k, т.е. А^k=RΛ^kR^-1,Λ^k=R^-1A^kR,

Подставляем А^k=RΛ^kR^-1 в (*), производя преобразования получаем:

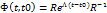
Алгоритм.

Отаскание собств. Знач. Матрицы А

Ищем собственные вектора 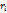, составляем матрицу R и находим R^-1

Находим Ф(t,t0)

Отыскание перех. матрицы с помощью обратного преобразования Лапласа

t0 = 0

,

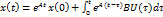Ф(t,0)=  =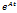

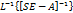
Еще один способ отыскания перех. Матрицы

x(t)=Ф(t,0)*x(0)

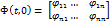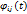,  - описание перех. Процесса по i-ой координате вектора состояния, при задании единичного нач. условия на j-ую координату, при остальных равных 0.

Еще один способ – отыскание через ряды.

Решение линейной нестационарной системы в пространстве состояний.

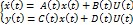
Найти решение x(t) начиная с некоторого момента времени t0 до ∞, представляющее собой траекторию в n- мерном пространстве, при задании входного воздействия U(t).

Решение ищем методом вариации постоянного, варьируя не скаляр, а векторную переменную.

Вектор состояния: 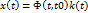,  k(t) – n – мерный вектор варьируемых параметров

Дифференцируем:

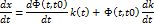
Подставляем x(t) в исходное уравнение:

 => =>

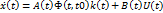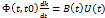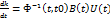
Вопрос существования 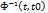закрывается теоремой:

На любом интервале времени, где A(t) интегрируема в смысле Римана, переходная матрица, удовлетворяющая свойству Ф(t,t0)=AФ(t,t0) является невырожденной.

Интегрируем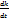

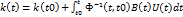, положим t=t0 (граничное условие)

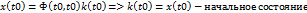
2.2)

Примеры нестационарных систем: Система наведения, автоматическая система посадки самолета.