2018-02-14
537
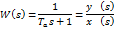
Соответствующее диффер. уравнение:
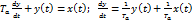Теперь можно воспользоваться одним из методов интегрирования. Воспользуемся методом Эйлера:
Входная функция, подлежащая интегрированию: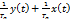 
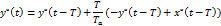
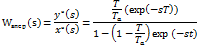
Структурная схема: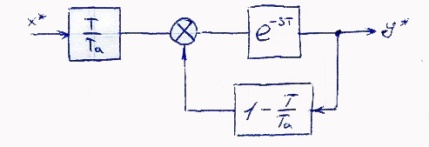 
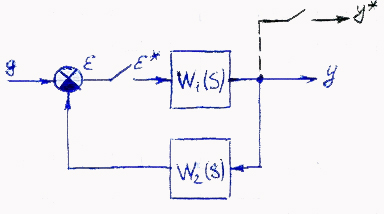
37.1) Передаточные функции дискретно-непрерывных систем на плоскости W*(s)
Рассмотрим отдельный фрагмент:
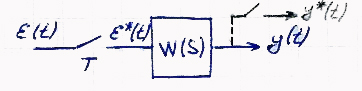
*(s)- дискретный сигнал
y(t)- непрерывный сигнал
y(s)=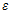 
*(s)·W(s); (s)=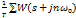 
Будем рассматривать непрерывный выходной сигнал только в тактовые моменты времени, это означает, что мы вводим фиктивный ключ, который замыкается одновременно с первым.
y*(s)= 
W*(s)=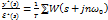 
Эта ПФ связывает импульсные сигналы на входе и фиктивном ключе. Теперь рассмотрим дискретно-непрерывную систему:
=g-V;
*=g*-V*;
Опять вводим фиктивный ключ
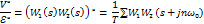
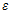*(s)=g*(s)-V*(s)=g*(s)- *(s)·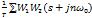 
Из последнего выражения видно, что можно вычислить ПФ ошибки:
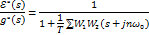
37.2) Сигнал на выходе: y(s)=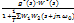 
; y*(s)= 
;
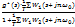Для дискретных систем есть два вида характеристического уравнения в зависимости от структуры.
1+W*p(j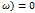 
Ключ после сигнала ошибки: W*p(j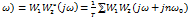 
Два ключа: Wp(j 
Чаще будем рассматривать структуры с одним ключом. Оказывается, что к такому описанию передаточной функции разомкнутой системы тоже будет применим критерий Найквиста.
38.1) Исследование устойчивости дискретно-непрерывных систем на плоскости s и W*(s).
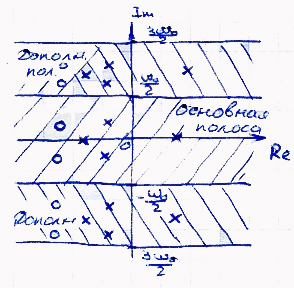
При построении годографа возникает особенность: известно, что функция W*(jω) является периодической с периодом 2π/Т, а значит годограф при построении от 0 до бескон. Будет повторяться, поэтому нужно рассм. годограф на отрезке (0;ω0), но лучше (-ω0/2; ω0/2). Можно построить годограф для положительной оси, а затем отобразить отн. действит. оси.
Точно поострить годограф из-за бесконечного числа слагаемых нельзя, поэтому ограничиваются теми, кот. дают наиб. вклад. n=0;-1;1 и.т.д.
Для исследования устойчивости дискретных систем применим критерий Найквиста. Допустим, что разомкнутая дискретная система устойчива, для того, чтобы замкнутая дискретная система была тоже устойчива, годограф не должен охватывать -1.
Существенный недостаток состоит в поведении годографа вблизи границы устойчивости,т.к. отброшенные слагаемые могут повлиять на годограф.
Пл-ть s.
У ПФ разомкнутой системы есть особенность: нули и полюса в силу периодических свойств все те же нули и полюса будут и во всех доп. полосах. критерий Найкв. работает на участке от 0 до ω0/2. Значит рассм. те нули и полюса, кот. попали в основную полосу справа. 38.2) допустим, полюс один, тогда для уст. замкн. дискр. системы нужно, чтобы год. при изм. Ω от 0 до ω0/2 охватил в полож. направлении полраза.
