Математический аппарат z-преобразований

При переходе от S к Z виду исчезает многозначность и удается избавиться от периодических свойств. Переход осуществляется заменой  (для дискретных сигналов только)

Свойства Z-преобразования:

1. Линейность

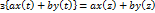
2. Сдвиг во времени на kT

3. Свойства частной производной

следует из равномерности сходимости ряда

4. Изменение масштаба в области z

5. Конечное значение x(t)->

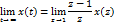
Лишь в том случае когда исследуется на устойчивость

6. Начальное значение

 

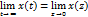
Вычисление z-преобразований сигналов и соответствующих передаточных функций.

 

1.

2.

3.

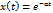
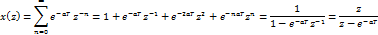
4.

40.2)

5.

6.

 

 

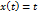
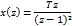
Описание дискретно-непрерывных систем с помощью передаточной функции W(z) и Ф(z).

 

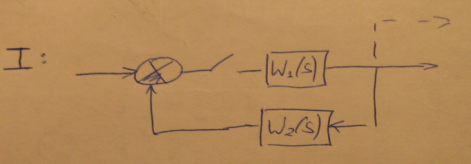
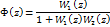
Построение годографаW(z).

Рассмотрим z=exp(TS), рассмотрим как преобразуется плоскость S в плоскость z.

Плоскость S:

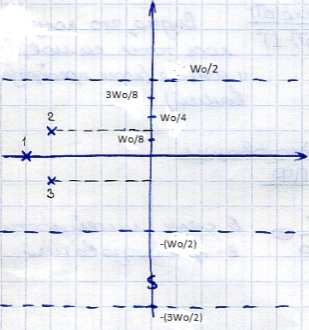
Плоскость Z:

Рассмотрим преобразование участка от 0 до /2:

0≤ w≤ /2: z=exp(Tjw) Этот участок в области z представляет собой единичную окружность, точнее верхнюю половину окружности.

Возьмём дополнительные точки: Wo/8, Wo/4, 3Wo/8

Wo/8: z=exp((2П/Wo)*Wj)=

42.2)

 

Особенности построения годографа дискретной системы:

-диапазон частот: 0≤ w≤ /2

-в место z подставляем t(Tjw), где T=2П/

Преимущества:

- В отличии от W*(S)-W(z)- функция детерминированная

- На плоскости S-бесчисленное число особенностей (полюсов), на плоскости z они не повторяются. Все полюса из дополнительных полос попадают в те же точки, что и точки из основной полосы. В общем, избавляемся от периодических повторений.

Критерий Найквиста работает в том же самом виде и на плоскости z.

43)

Билинейное преобразование. Понятие псевдочастотных характеристик.

 

Билинейное преобразование п.ф. W(Z) получается при замене Z = (1 + (T/2)S_)/(1 – (T/2)S_).

S_=jw_, где w_ - псевдочастота.

Для системы на плоскости S_, так же, как и на пл. S, можно использовать ЛАФЧХ, АФЧ годограф, корневой годограф.

 

S_ = (2/T)*(Z-1)/(Z+1)

S_ = (2/T)*th(ST/2)

S_ = j(2/T)*tg(wT/2) = jw_

w_ = (2/T)*tg(wT/2)

 

горизонтальная сетка при переходе из пл.S в пл.S_ сохраняет ортогональность, линии переходят в окружности конечного или бесконечного радиуса.