
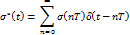
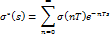
Прохождение сигнала через экстраполятор:
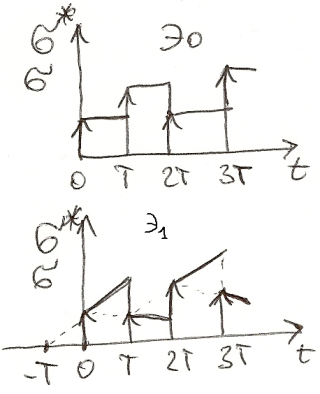
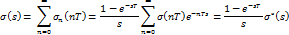
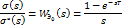
30.1)Преобразование спектров сигнала при прохождении через импульсный элемент Рассм. частотный (подход) метод к преобразователям К-А и А-К
Т.к. 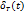 явл. периодической (с периодом T), то её частотное представление м.б. представлено в виде ряда Фурье в комплексной форме:
явл. периодической (с периодом T), то её частотное представление м.б. представлено в виде ряда Фурье в комплексной форме:
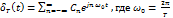 , n – номер гармоники
, n – номер гармоники
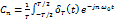 dt =
dt = 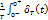 *1dt =
*1dt =  , т.е.
, т.е. 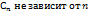
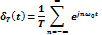
Спектр импульсной последовательности: 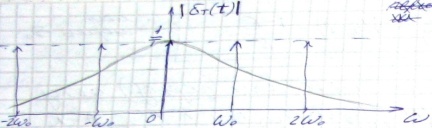 Идеализация. Для импульсов реальный спектр будем использовать идеализированное
Идеализация. Для импульсов реальный спектр будем использовать идеализированное
Представление.
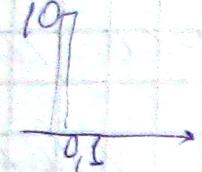 Рассм. на входе преоб-ля аналог-код непр-й гармонич. cигнал:
Рассм. на входе преоб-ля аналог-код непр-й гармонич. cигнал:
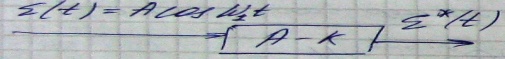
30.2) 
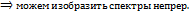
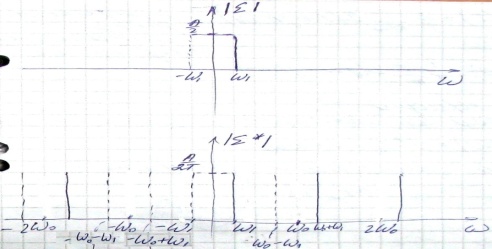
Спектр становится периодическим (транспонирование частот) – эффект при дискретизации, т.е. спектр размножается.
Подадим на вход преоб-ля непр. сигнал 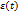 , не явл-ся периодической ф-цией
, не явл-ся периодической ф-цией
(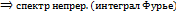 )
)
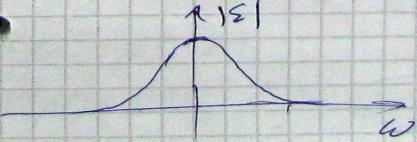 - спектр непрерывного сигнала
- спектр непрерывного сигнала

Достоверного воспроизведения исх. непрер. сигнала мы не получим (искажение)
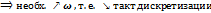
Теорема Котельникова: Частота дискретизации д.б. по-крайней мере в 2 раза больше, чем самая большая частота в спектре сигнала
Частотные характеристики экстраполятора нулевого порядка
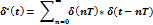
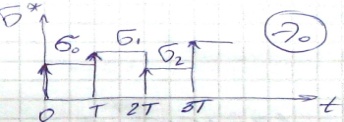 На входе К-А необходимо запомнить вх.сигнал до наступления следующего (на всём интервале) – это называется устройство экстраполятор 0-го порядка (не учитывается производная
На входе К-А необходимо запомнить вх.сигнал до наступления следующего (на всём интервале) – это называется устройство экстраполятор 0-го порядка (не учитывается производная
Частотный спектр преобразователя “код-аналог”.
Его передаточная функция: 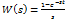
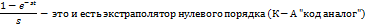
Заменяем s на j  :
: 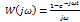

Переходим к половинному аргументу, домножая на 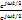 :
:
= 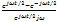 *
* 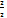 =
= 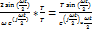 ,
, 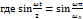
Теперь легко найти модуль и фазу:
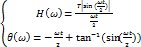 ,где
,где 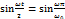
31.2)
В линейном масштабе:

В логарифмическом масштабе:

 2018-02-14
2018-02-14 304
304








