Если Fрасч>Fкр, то модель адекватна статистическим данным (хотя бы один из параметров при Х не равен нулю).
- F-расчетное:

 находим в ячейке B98 по формуле =N22/(M22/14)
находим в ячейке B98 по формуле =N22/(M22/14)
 = 3051,505984
= 3051,505984
- F-критическое
Fкр находится с помощью функции FРАСПОБР
уровень значимости – 0,05;
степень свободы 1 – m=1;
степень свободы 2 – n-m-1=16-1-1=14
Fкр находим в ячейке В97.
Fкр = 4,600109908
Так как Fрасч>Fкр, то модель адекватна статистическим данным.
Точечный прогноз:
 .
.
В ячейку І19 вводим формулу =$A$86+B19*$A$87
Расчет доверительного интервала
 , где
, где

Найдем 
1. 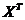 - транспонирование матрицы Х;
- транспонирование матрицы Х;
2. 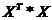 - результат (1) умножить на матрицу Х;
- результат (1) умножить на матрицу Х;
3.  - найти обратную матрицу к результату (2);
- найти обратную матрицу к результату (2);
4.  -
-  умножить на результат (3)
умножить на результат (3)

5. Расчитываем  .
.
6.  - результат (4) умножить на
- результат (4) умножить на 
7.  .
.
8. Рассчитываем  . В ячейку В133 вводим формулу =КОРЕНЬ(M22/14)
. В ячейку В133 вводим формулу =КОРЕНЬ(M22/14)
9.  . В ячейку В134 вводим формулу =A131*B133*B100
. В ячейку В134 вводим формулу =A131*B133*B100
Ymin = 39,9703959
Ymax = 41,73342534
Частичный коэффициент эластичности рассчитываем по формуле:

Частичный коэффициент эластичности показывает на сколько процентов изменится показатель Y при неизмененных значениях других факторов, если X1 изменится на 1%.

Выводы:
1. Между факторами Х1, Х2 и Х3 существует мультиколлинеарность. Выбросим факторы Х2, Х3, так как они менее всего влияют на показательУ.
2. Так как Fрасч>Fкр, то с надежностью 0,95 можна считать модель  адекватной статистическим данным. На основании этой модели можно делать экономические выводы.
адекватной статистическим данным. На основании этой модели можно делать экономические выводы.
3. С надежностью 0,95 можно считать, что влияние фактора Х1 на показатель У значительное.
4. Прогнозное значение показателя с надежностью 0,95 будет находится в промежутке [39,9703959; 41,73342534]
5. При изменении факторов в точке пргноза Х1р на 1 % показатель У изменится на 0,862414917 %.
Приложение
Таблица 1
Множественная линейная регрессия


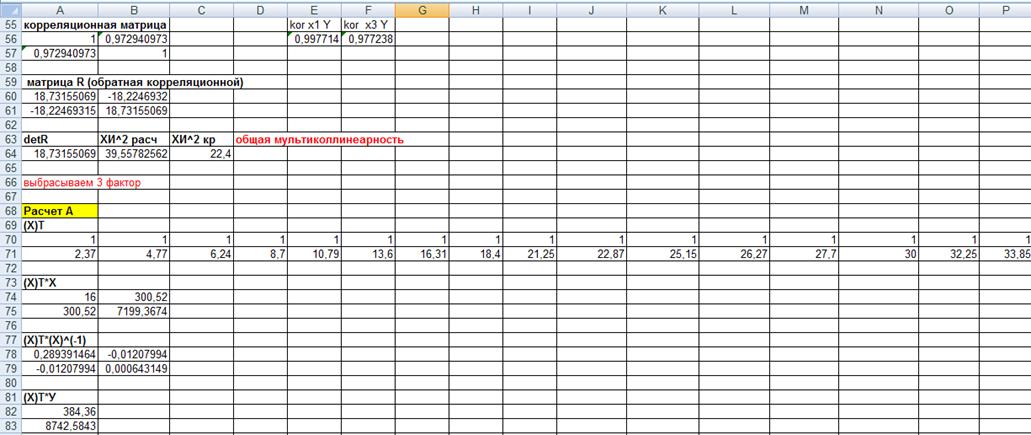


Таблица 2
Режим формул





 2018-02-14
2018-02-14 908
908







