Тест на наличие мультиколлинеарности

Построение корреляционной матрицы

Корреляционная матрица имеет вид:

Корреляционная матрица симметрична, по главной диагонали. Все элементы главной диагонали равны 1.

Расчет корреляционной матрицы:

- При помощи встроенной функции КОРРЕЛ:

Корреляционная матрица рассчитана в блоке A24:C26.

Таблица 1

Корреляционная матрица

1	0,992929	0,97294097
	1	0,98701797
		1

 

 

- Корреляционную матрицу находят по формуле:

Размер полученной матрицы:

- матрица нормализованных статистических данных, которая имеет вид:

Элементы данной матрицы находятся по формуле:

Таблица 2

Матрица нормализованных статистических данных

X1 норм	X2 норм	X3 норм
-0,41623	-0,45755	-0,46946
-0,35536	-0,38141	-0,35692
-0,31808	-0,28576	-0,30977
-0,2557	-0,25054	-0,2824
-0,20269	-0,21914	-0,15693
-0,13143	-0,12349	-0,15541
-0,0627	-0,04021	-0,0634
-0,0097	0,026886	0,105412
0,062577	0,097791	0,097807
0,103661	0,126818	0,154078
0,161482	0,127294	0,126703
0,189886	0,233413	0,305399
0,226151	0,23484	0,186775
0,28448	0,24864	0,210348
0,341541	0,296227	0,248368
0,382117	0,366179	0,359388

 

Транспонируем матрицу . Для этого выделяем ячейки A28:P30. В ячейку А28 вводим формулу =ТРАНСП(F3:H18).

Найдем произведение  и поместим в ячейки A33:C35. Вводим формулу =МУМНОЖ(A28:P30;F3:H18).

 В блоке А33:С35 мы получили корреляционную матрицу вторым способом.

 

Тест на наличие мультиколлинеарности

1. Проверяется наличие или отсутствие общей мультиколлинеарности в модели при помощи χ²-критерия Пирсона.

Если > 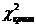в модели имеется общая мультиколлинеарность с доверительной вероятностью 0,95.

 

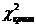 находят в таблице «Критические точки распределения χ²»

- уровень значимости 0,05;

- степени свободы 1/2m(m-1)=1/2*3*(3-1)=3.

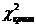 = 21.

 

, где

n - количество показателей;

m - количество факторов;

R=K^-1, R - матрица, обратная к матрице К;

К – корреляционная матрица.

Найдем матрицу обратную к корреляционной. Для этого вводим формулу =МОБР(A33:C35) в ячейку А38. В ячейке A43 находим определитель матрицы R по формуле =МОПРЕД(A38:C40).

 находим в ячейке C43 по формуле =(16-1-11/6)*LN(A43)

= 106,240274.

Так как > 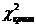в модели имеется общая мультиколлинеарность с доверительной вероятностью 0,95.

 

2. Так как в модели имеет место мультиколлинеарность, необходимо выяснить между какими факторами она присутствует

Если t_расч >t_кр, то между рассматриваемыми двумя факторами имеет место мультиколлинеарность.

t_кр находят при помощи функции СТЬДРАСПРОБР:

- уровень значимости – 0,05/2;

- степени свободы –   n-m-1=16-3-1=12

t_кр = 2,178813.

 

t_расч рассчитывается по формуле:

;

 - частичный коэффициент корреляции.

Частичный коэффициент корреляции  показывает тесноту линейной связи между первым и вторым фактором, когда третий фактор зафиксирован, то есть его влияние исключено.

,

 

- элементы матрицы R (R=K^-1)

 

Таблица 3

Частичный коэффициент корреляции

r12,3=	0,878986
r13,2=	-0,37227
r23,1=	0,764051

 

На основании частичного коэффициента корреляции рассчитаем t_расч

Таблица 4

Т-статистика

t12,3=	6,385478
t13,2=	-1,38947
t23,1=	4,102499

 

Так как t_12.3>t_кр, то между 1 и 2 факторами имеет место мультиколлинеарность

Так как t_23.1>t_кр, то между 2 и 3 факторами имеет место мультиколлинеарность.

Таким образом из модели выбрасываем 2 фактор.

Построим вторую корреляционную матрицу при помощи встроенной функции КОРРЕЛ.

Таблица 5

Корреляционная матрица

1	0,972941
0,972941	1