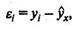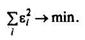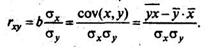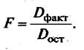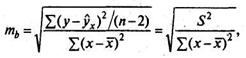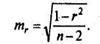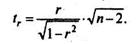2018-02-14
490
Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели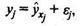 
где yj — фактическое значение результативного признака;
ŷ xj. - теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и x, т. е. из уравнения регрессии;
εj — случайная величина (возмущение), характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Ее присутствие в модели порождено тремя источниками: спецификацией модели (а) неправильный выбор той или иной математической функции, б) недоучет в уравнении регрессии какого-либо существенного фактора), выборочным характером исходных данных (если совокупность неоднородна, то уравнение регрессии не имеет практического смысла), особенностями измерения переменных (например, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например в результате наличия сокрытых доходов).
|
|
|
В парной регрессии выбор вида математической функции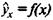 
может быть осуществлен тремя методами:
• графическим;
• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
• экспериментальным.
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида
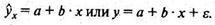
Построение линейной регрессии сводится к оценке ее параметров - а и b. Оценки параметров линейной регрессии могут быть найдены разными методами.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических)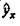 
минимальна: 
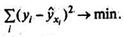Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:
|
|
следовательно,
|
|
То есть, получим следующую систему нормальных уравнений для оценки параметров а и b:
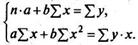
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Формально а — значение у при x = 0. Если признак-фактор x не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла.
|
|
|
Уравнение регрессии всегда дополняется показателем тесноты связи. Существуют разные модификации формулы линейного коэффициента корреляции:
|
|
Как известно, линейный коэффициент корреляции находится в границах: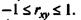 
Если коэффициент регрессии b > 0, то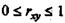 
, и, наоборот, при b < 0,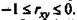 
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r2xy, называемый коэффициентом детерминации.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b= 0, и, следовательно, фактор x не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения yна две части — «объясненную» и «необъясненную». Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.
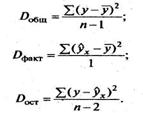
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения (F-критерий):
|
|
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: тb и та.
Стандартная ошибка коэффициента регрессии определяется по формуле
|
|
где S2 — остаточная дисперсия на одну степень свободы.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдента: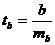 
, которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n - 2).
Стандартная ошибка параметра а определяется по формуле:
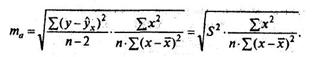
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: ta = a/ma, его величина сравнивается с табличным значением при df = n - 2 степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr.
|
|
Фактическое значение t-критерия Стьюдента определяется как
|
|
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз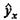 
при хр =хк, т. е. путем подстановки в уравнение регрессии 
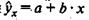соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом интегральной ошибки прогноза ЕY, которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии - 
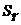и ошибки прогноза положения регрессии 
.
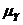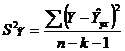
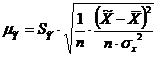
Интегральная ошибка прогноза составит:
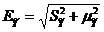
Предельная ошибка прогноза (при уровне значимости 0,05) составит:
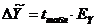
Табличное значение определили по таблице распределения Стьюдента с учетом значимости 0,05 и числом степеней свободы v = n-2.
Фактическая реализация прогноза будет находиться в доверительном интервале: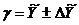 
. Относительная величина различий значений верхней и нижней границ характеризует точность выполненного прогноза.
Различают два класса нелинейных регрессий:
|
|
|
• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. К этому классу относятся полиномы различных степеней, равносторонняя гипербола. Параметры определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам.
• регрессии, нелинейные по оцениваемым параметрам. К этому классу относятся следующие функции: степенная, показательная, экспоненциальная и др.
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция y = а · x^b · ε. Связано это с тем, что параметр bв ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента bпоказывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.
В силу того что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле
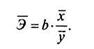
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R):
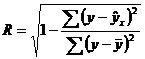
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции.
|
|
|
Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:
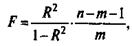
где R2 - индекс детерминации;
n - число наблюдений;
т — число параметров при переменных х.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую.
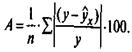
Ошибка аппроксимации в пределах 5—7 % свидетельствует о хорошем подборе модели к исходным данным.
