Тема 4. Множественная регрессия и корреляция

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Она включает в себя два круга вопросов: отбор фак­торов и выбор вида уравнения регрессии.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требова­ниям.

1. Они должны быть количественно измеримы. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

3. Включаемые факторы не должны коррелировать друг с другом. Наибольшие труд­ности в использовании аппарата множественной регрессии воз­никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос­тью, т. е. имеет место совокупное воздействие факторов друг на друга.

Наличие мультиколлинеарности между признаками приводит к:

· Искажению величины параметров модели, которые имеют тенденцию к завышению;

· Изменению смысла экономической интерпретации коэффициентов регрессии;

· Слабые обусловленности системы нормальных равнений;

· Осложнению процесса определения наиболее существенных факторных признаков.

В решении проблемы мультиколлинеарности моно выделить несколько этапов:

· Установление наличия мультиколлинеарности;

· Определение причин возникновения мультиколлинеарности;

· Разработка мер по её устранению.

Причинами возникновения мультиколлинеарности между призанками являются:

· Изучаемые факторные признаки, характеризующие одну и ту же сторону явления или процесса. Например, показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия;

· Использование в качестве факторных признаков показателей, суммарное значение которых представляет собой постоянную величину;

· Факторные признаки, являющиеся составными элементами друг друга;

· Факторные признаки, по экономическому смыслу дублирующие друг друга.

Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8 (r_{xi xj}) и др.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов рег­рессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения ре­грессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

• метод исключения;

• метод включения;

• шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты — отсев факторов из полного его набора (метод исключения), дополнительное введе­ние фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

Практика построения многофакторных моделей взаимосвязи показывает, что все реально существующие зависимости между социально экономическими явлениями можно описать используя пять типов моделей:

₁₎ Линейная: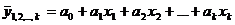

2) Степенная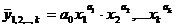    

3) Показательная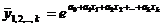

4) Параболическая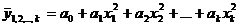

5) Гиперболическая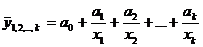

Наиболее приемлемым способом определения вида исходного уравнения регрессии является метод перебора различных уравнений.  

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные формы зависимости приводятся к линейным путем линеаризации. В линейной мно­жественной регрессии 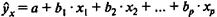парамет­ры при xназываются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соот­ветствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Параметры уравнения множественной регрессии оценивают­ся, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки пара­метров регрессии.

Уравнение множественной регрессии можно построить в естественном и стандартизированном виде.

А) Построение уравнения в естественном виде. Так, для уравнения у = а + b ₁ · х₁ + b₂ · х₂ + ··· + b_р · х_р + ε сис­тема нормальных уравнений составит:

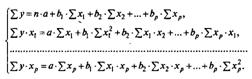
Ее решение может быть осуществлено методом определителей:

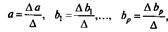
где         Δ — определитель системы;

Δ а, Δ b₁,..., Δ b_p — частные определители.

Б) Возможен и иной подход к определению параметров множе­ственной регрессии, когда на основе матрицы парных коэффи­циентов корреляции строится уравнение регрессии в стандарти­зованном масштабе:

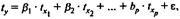
где 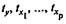— стандартизованные переменные: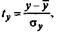

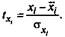
для которых среднее значение равно нулю:

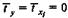
а среднее квадратическое отклонение равно единице:

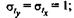    β -стандартизованные коэффициенты регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобра­зований получим систему нормальных уравнений вида

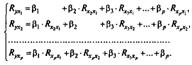
Решая ее методом определителей, найдем параметры — стан­дартизованные коэффициенты регрессии (β -коэффициенты).

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответст­вующий фактор x _j, изменится на одну сигму при неизменном среднем уровне других факторов. Сравнивая их друг с другом, можно ранжировать факторы по си­ле их воздействия на результат.

От уравнения в стандартизированном виде можно перейти к уравнению в естественной форме. Так, переход для двухфакторного уравнения множественной регрессии можно записать следующим образом:

   

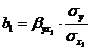
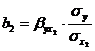
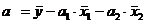
Практическая значимость уравнения множественной регрес­сии оценивается с помощью показателя множественной корре­ляции и его квадрата - коэффициента детерминации.

Показатель множественной корреляции характеризует тесно­ту связи рассматриваемого набора факторов с исследуемым при­знаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной кор­реляции может быть найден как индекс множественной корре­ляции:

 

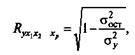
где  σ² _у — общая дисперсия результативного признака;

       σ² _ост - остаточная дисперсия для уравнения y =f(x₁, x ₂,..., x _p).

 

При линейной зависимости признаков формула индекса кор­реляции может быть представлена следующим выражением:

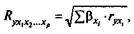
где β_xi - стандартизованные коэффициенты регрессии;

   r _уxi   -парные коэффициенты корреляции результата с каждым фактором.

Скорректированный индекс множественной корреляции со­держит поправку на число степеней свободы, а именно остаточ­ная сумма квадратов 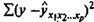делится на число степеней свободы остаточной вариации (n - т - 1), а общая сумма квадра­тов отклонений  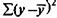- на число степеней свободы в целом по совокупности (n - 1).

Формула скорректированного индекса множественной детер­минации имеет вид:

 

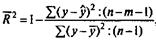
где т - число параметров при переменных х;

 n - число наблюдений.

Поскольку 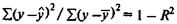, то величину скорректированного индекса детерминации можно представить в виде

 

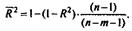
Чем больше величина m, тем сильнее различия 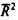и R².

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных(без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

Частные коэффициенты корреляции. Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень влияния одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-кри­терия Фишера:

 

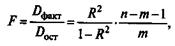
где D _факт - факторная сумма квадратов на одну степень свободы;

D _ост - остаточная сумма квадратов на одну степень свободы;

R²- коэффициент (индекс) множественной детерминации;

т - число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов);

 n- число наблюдений.

Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Частный F-критерий построен на сравнении прироста фак­торной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния x₁ как дополнительно включен­ного в модель фактора. Используем следующую формулу:

 

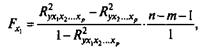
где R² _yx1x2...xp - коэффициент множественной детерминации для модели с полным набором факторов;

R²_yx2....xp ~ тот же показатель, но без включения в модель фактора x₁;

n- число наблюдений;

  т - число параметров в модели (без свободного члена).

Фактическое значение частного F-критерия сравнивается с табличным при 5%-ном или 1%-ном уровне значимости и числе степеней свободы: 1 и n— т — 1. Если фактическое значение F_xj. превышает 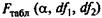, то дополнительное включение фактора x_j в модель статистически оправданно и коэффициент чис­той регрессии b _i при факторе x_i - статистически значим. Если же фактическое значение F_xj меньше табличного, то дополнитель­ное включение в модель фактора х, не увеличивает существенно долю объясненной вариации признака у, следовательно, нецеле­сообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

С помощью частного F-критерия можно проверить значи­мость всех коэффициентов регрессии в предположении, что каж­дый соответствующий фактор x_i - вводился в уравнение множест­венной регрессии последним.

Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента может быть проведена и без расчета част­ных F-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула

 

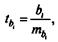
где b₁ — коэффициент чистой регрессии при факторе x_j;

     т_bi — средняя квадратическая ошибка коэффициента регрессии b_i

Для уравнения множественной регрессии 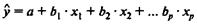 средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:

 

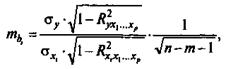
где σ_у - среднее квадратическое отклонение для признака у;

   σ_xi - среднее квадратическое отклонение для признака x_i;

  R² _yx1...xp - коэффициент детерминации для уравнения множественной регрессии;

      R² _xix1...xp- коэффициент детерминации для зависимости фактора x_t со всеми другими факторами уравнения множественной регрессии;

    n - т - 1 - число степеней свободы для остаточной суммы квадратов отклонений.

До сих пор в качестве факторов рассматривались экономиче­ские переменные, принимающие количественные значения в не­котором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качествен­ных уровней. Что­бы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. каче­ственные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В отечественной литературе можно встретить термин «структурные переменные».

При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей ε.

 В модели

y=а+b₁∙x₁+b₂∙x₂+…+b_p∙x_p+ε

случайная составляющая ε представляет собой ненаблюдаемую величину. После того как произведена оценка параметров моде­ли, рассчитывая разности фактических и теоретических значе­ний результативного признака у, можно определить оценки слу­чайной составляющей y — 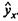. Поскольку они не есть реальные случайные остатки, их можно считать некоторой выборочной ре­ализацией неизвестного остатка заданного уравнения, т. е. ε_j.

При изменении спецификации модели, добавлении в нее но­вых наблюдений выборочные оценки остатков ε_j могут меняться. Поэтому в задачу регрессионного анализа входит не только пост­роение самой модели, но и исследование случайных отклонений ε_j, т. е. остаточных величин.

Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является жела­тельным свойством, так как только в этом случае они могут иметь практическую значимость. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оцениваний остатки не будут на­капливаться и найденный параметр регрессии b_i можно рассмат­ривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несме­щенности, то их можно сравнивать по разным исследованиям.

Для практических целей важна не только несмещенность, но и эффективность оценок. Оценки считаются эффективными, ес­ли они характеризуются наименьшей дисперсией. Поэтому не­смещенность оценки должна дополняться минимальной диспер­сией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

Степень реалистичности доверительных интервалов парамет­ров регрессии обеспечивается, если оценки будут не только не­смещенными и эффективными, но и состоятельными. Состоя­тельность оценок характеризует увеличение их точности с увели­чением объема выборки. Большой практический интерес пред­ставляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии b_i имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от ис­тинного значения параметра близка к единице.

Указанные критерии оценок (несмещенность, состоятель­ность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов ос­татков. Поэтому очень важно исследовать поведение остаточных величин регрессии ε _i. Условия, необходимые для получения не­смещенных, состоятельных и эффективных оценок, представля­ют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Исследования остатков ε_i - предполагают проверку наличия сле­дующих пяти предпосылок МНК:

• случайный характер остатков;

• нулевая средняя величина остатков, не зависящая от х_i;

• гомоскедастичность — дисперсия каждого отклонения ε _i
одинакова для всех значений х;

• отсутствие автокорреляции остатков. Значения остатков ε _i
распределены независимо друг от друга;

• остатки подчиняются нормальному распределению.

В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и по методу максимального прав­доподобия, совпадают между собой. Если распределение случай­ных остатков ε _i не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Прежде всего проверяется случайный характер остатков ε _i -первая предпосылка МНК.

С этой целью стоится график зависимости остатков ε _i - от тео­ретических значений результативного признака (рис.).

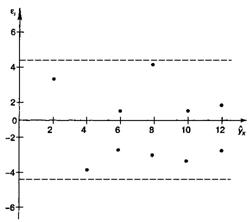
Рис. Зависимость случайных остатков ε _i от теоретических значений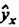

 

Если на графике получена горизонтальная полоса, то остатки ε _i представляют собой случайные

В этих случаях необходимо либо применять дру­гую функцию, либо вводить дополнительную информацию и за­ново строить уравнение регрессии до тех пор, пока остатки ε _i не будут случайными величинами.

Вторая предпосылка ΜΗΚ относительно нулевой средней ве­личины остатков означает, что 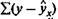= 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю­чаемых переменных. Для моделей, нелинейных по оцениваемым параметрам и приводимых к линейному виду логарифмировани­ем, средняя ошибка равна нулю для логарифмов исходных дан­ных.

Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений x_j. Если же график показывает наличие зависимости ε _i и х_j, то модель неадек­ватна. Корреляция случайных остатков с факторными признаками позволяет проводить корректировку модели, в частности использовать кусочно-линейные модели.

Предпосылка о нормальном распределении остатков позво­ляет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Вместе с тем оценки регрессии, найден­ные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки МНК.

Совершенно необходимым для получения по МНК состоя­тельных оценок параметров регрессии является соблюдение тре­тьей и четвертой предпосылок.

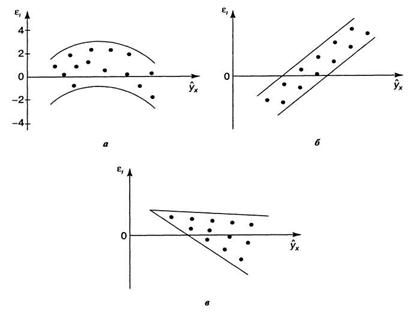
В соответствии с третьей предпосылкой МНК требуется, что­бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора х_j остатки ε _i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.

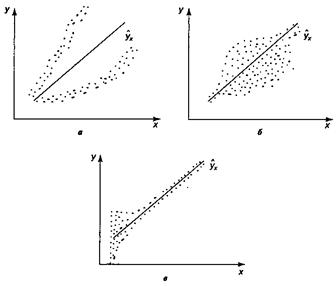
Рис. Примеры гетероскедастичности:

а — дисперсия остатков растет по мере увеличения х;

б — дисперсия остатков достигает максимальной величины при средних

значениях переменной xи уменьшается при минимальных

и максимальных значениях х;

в — максимальная дисперсия остатков при

малых значениях xи дисперсия остатков однородна

по мере увеличения значений x

Гомоскедастичность остатков означает, что дисперсия остат­ков ε _i одинакова для каждого значения х. Используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо - и гетероскедастичность.

 

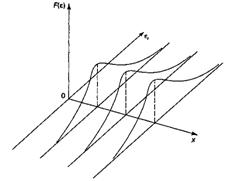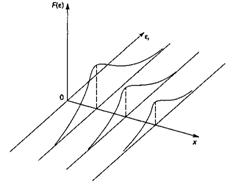Рис.Гомоскедастичность остатков

Рис. Гетероскедастичность остатков

Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков ε _i от теоретических значений результативного признака .

Наличие гетероскедастичности может в отдельных случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии в основном зависит от соблюдения второй предпосылки МНК, т. е. незави­симости остатков и величин факторов. Гетероскедастичность бу­дет сказываться на уменьшении эффективности оценок b_i.

При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастич­ности может использоваться метод Гольдфельда — Квандта, раз­работанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков воз­растает пропорционально квадрату фактора. Чтобы оценить на­рушение гомоскедастичности, они предложили параметрический тест, который включает в себя следующие шаги.

1. Упорядочение n наблюдений по мере возрастания переменной х.

2. Исключение из рассмотрения С центральных наблюдений; при этом (n — С): 2 > p, где p— число оцениваемых параметров.

3. Разделение совокупности из (n - С) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

4. Определение остаточной суммы квадратов для первой (S₁) и второй (S₂) групп и нахождение их отношения: R = S₁: S₂ .

При выполнении нулевой гипотезы о гомоскедастичности от­ношение R будет удовлетворять F-критерию с (n - С - 2р): 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрес­сии, которые обладают свойством несмещенности, имеют мень­шее значение дисперсии остатков и обеспечивают в связи с этим более эффективную статистическую проверку значимости пара­метров регрессии. Этой цели, как уже указывалось, служит и при­менение обобщенного метода наименьших квадратов.