Гармонический осциллятор

1 2 3 4 5 6

Дифференциальное уравнение гармонических колебаний материальной точки для координаты:

Дифференциальное уравнение гармонических колебаний маятника для угла отклонения от вертикали:

Гармонические колебания:

Циклическая частота незатухающих колебаний физического маятника (собственная частота):

Циклическая частота незатухающих колебаний математического маятника (собственная частота):

Период колебаний:

Частота колебаний:

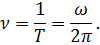
Дифференциальное уравнение затухающих колебаний материальной точки для координаты:

где – коэффициент затухания.

Затухающие колебания:

Циклическая частота затухающих колебаний:

Декремент затухающих колебаний:

логарифмический декремент затухающих колебаний:

Колебания груза на пружине.

Если к пружине подвешен груз массы ,пружина может находиться в равновесии, когда сила тяжести по модулю будет равна силе упругости:

При этом пружина будет растянута на величину :

Ось построим вертикально, а нулевую координату разместим на уровне, соответствующем положению равновесия груза. Высоту груза на этом уровне обозначим .

Если груз вывести из состояния равновесия, то сила упругости по модулю станет больше силы тяжести при и меньше силы тяжести при . Неупругими силами пренебрегаем. При этом уравнение второго закона Ньютона в проекции на ось :

где циклическая частота колебаний

Груз на пружине будет совершать колебания по закону

где начальная координата зависит от начального положения груза.

Механическая энергия груза:

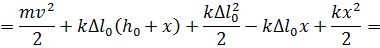
Начальную потенциальную энергию можно принять равной нулю. Тогда

Механическая энергия груза в процессе колебаний не изменяется, .

Скорость груза достигает максимального значения при , координата достигает максимального значения при .

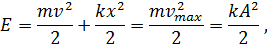
185. Координата колеблющейся точки зависит от времени по закону 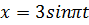, см. Найдите среднюю скорость точки за первую четверть периода ее колебаний.

Решение.

Циклическая частота колебаний , а период колебаний

Согласно условию точка начинает колебание из положения равновесия ( при ) и первую четверть периода будет двигаться в одну сторону, пройдя расстояние

Средняя скорость при этом

189. Колебания совершаются по закону . В момент времени смещение составляет половину амплитуды. Найдите начальную фазу колебаний.

Решение.

Согласно условию

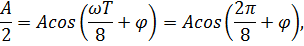
откуда

199. Период малых вертикальных колебаний шарика, подвешенного на легкой пружине в воздухе, равен 1 с. При погружении шарика в вязкую жидкость период его колебаний увеличивается на 10 %. Найдите коэффициент затухания колебаний.

Решение.

Используем формулы:

Согласно условию

203. Куб массой 4 кг с ребром 10 см подвешен за одну из вершин и совершает гармонические колебания относительно горизонтальной оси с частотой 2,19 Гц. Найдите момент инерции куба относительно оси колебаний.

Решение.

Частота незатухающих колебаний физического маятника (собственная частота):

откуда

Для нахождения момента инерции куба относительно оси колебаний нужно сначала найти расстояние от точки подвеса до центра масс куба. Для нахождения этого расстояния нарисуем диагональное сечение куба.

Как видно из рисунка,

Итак,

205. Спустя 0,25 с после начала движения кинетическая энергия точки, колеблющейся по закону , составляет 25 % ее полной механической энергии. Найдите начальную фазу колебаний, если их период равен 2 с.

Решение.

Для вычисления кинетической энергии нужно найти скорость колеблющейся точки:

откуда кинетическая энергия:

Согласно условию

Эта задача имеет бесчисленное множество решений. В качестве ответа можно привести два значения начальной фазы: . Все другие значения отличаются от выбранных на целое число .

210. Затухающие колебания происходят по закону . В момент времени 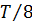скорость колеблющегося тела в первый раз равна нулю. Найдите отношение круговой частоты колебаний к коэффициенту затухания.

Решение.

Найдем скорость колеблющейся точки:

Согласно условию

211. Найдите логарифмический декремент затухания для математического маятника длиной 80 см, если коэффициент затухания равен 0,8.

Решение.

Логарифмический декремент затухания равен

Для нахождения логарифмического декремента затухания нужно найти период колебаний.

212. Груз, подвешенный на легкой пружине, растягивает ее на 10 см. Найдите период вертикальных колебаний груза на этой пружине, если логарифмический декремент затухания колебаний равен 3,14.

Решение.

Собственная частота незатухающих колебаний равна