2018-02-14
2187
Молекулы воздуха в атмосфере Земли распределены неравномерно. С одной стороны, газ стремится занять весь предоставленный объём, с другой – действует притяжение к Земле. В результате действия этих двух конкурирующих факторов:
1) теплового движения;
2) притяжения Земли
устанавливается стационарное распределение молекул по высоте. Давление газа с высотой уменьшается по некоторому закону. Найдём его, предполагая, что:
1) газ – идеальный (подчиняется уравнению Менделеева-Клапейрона);
2) температура постоянна: 
;
3) поле тяготения однородно: 
.
Рассмотрим вертикальный столб газа с площадью основания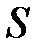 
(рис.6.12). Давление на высоте 
обозначим 
; на высоте 
давление равно 
(очевидно, 
). На слой толщиной 
и массой 
, находящийся в равновесии, действуют силы:
1) 
– сила тяжести, её величину можно выразить через плотность газа и объём слоя 
:
;
2) 
– сила давления на высоте , направлена сверху вниз;
3) 
– сила давления на высоте , направлена снизу вверх.
| Рис.6.12 |
Слой находится в равновесии, то есть силы, действующие на него, уравновешивают друг друга: 
,
или в проекциях на вертикальную ось:
. (6.53)
Тогда
.
Далее, после сокращения:
. (6.54)
Газ – идеальный; запишем уравнение Менделеева-Клапейрона:
, тогда из (6.54): 
.
Последнее уравнение проинтегрируем по высоте, учтя, что и :
;
(6.54)
Поскольку 
, то 
. (6.54а)
Это – барометрическая формула, показывающая, как давление уменьшается с высотой в поле силы тяжести.
Используя барометрическую формулу, найдём закон уменьшения концентрации молекул с высотой. Поскольку для идеального газа 
, 
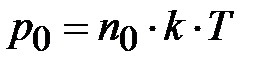, а произведение 
– потенциальная энергия молекулы в поле силы тяжести, то
. (6.55)
Полученное для молекул в однородном поле силы тяжести распределение Больцмана (6.55) универсально: годится для частиц, находящихся в любом потенциальном поле. Из (6.55) найдём отношение концентраций 
и 
частиц в двух точках 1 и 2:
. (6.56)
Величина 
показывает, во сколько раз отличаются концентрации частиц в двух точках потенциального поля, если их потенциальные энергии отличаются на 
. Знак «минус» в (6.56) означает, что концентрация больше в тех точках, где потенциальная энергия меньше: всякая система с большей вероятностью будет находится в состоянии с наименьшей потенциальной энергией.
Распределение (6.56) – это распределение частиц по координатам, потому что потенциальная энергия зависит от координат частицы: 
. Можно объединить распределения по скоростям и по координатам. Пусть 
– доля частиц с координатами:
;
;
;
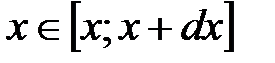и с проекциями скоростей:
;
;
;
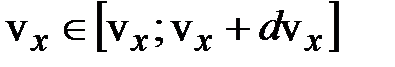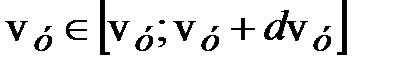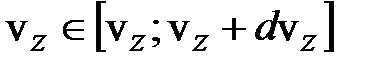тогда по закону умножения вероятностей из (6.43) и (6.56):
,
где 
– полная энергия частицы.
Билет
