Пусть точка одновременно участвует в двух колебаниях одинаковой частоты:
 ,
,
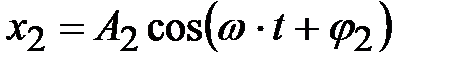 ,
,
тогда результирующее смещение точки из положения равновесия тоже будет гармоническим колебанием с той же частотой:
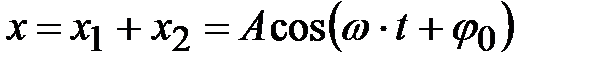 .
.
| Рис.4.8 |
 Найдём амплитуду и начальную фазу этого колебания по методу векторных диаграмм (рис. 4.8).
Найдём амплитуду и начальную фазу этого колебания по методу векторных диаграмм (рис. 4.8). 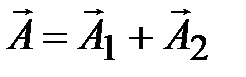 ;
;
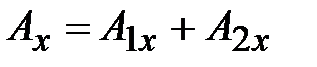 ;
; 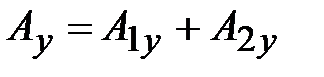 ;
;
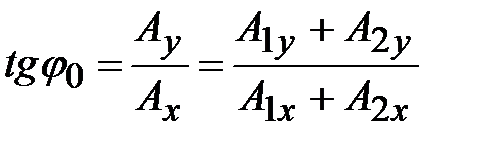 ;
;
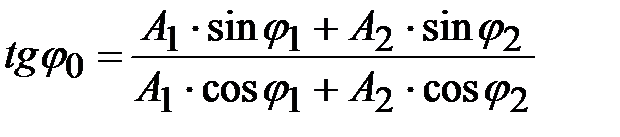 ; (4.19)
; (4.19)
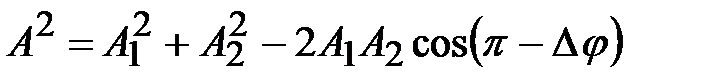 ,
,
где  ;
;
 . (4.20)
. (4.20)
При сложении не двух, а большего числа колебаний одинаковой частоты
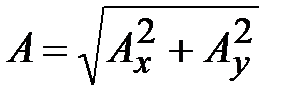 ,
,
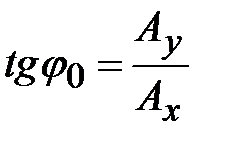 ,
,
где 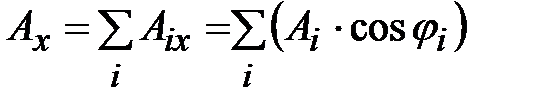 ;
; 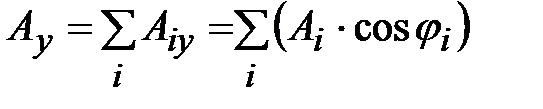 .
.
Частные случаи: 1) если сдвиг фаз колебаний 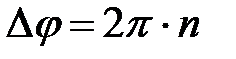 , где n – целое число (колебания происходят в одной фазе), то
, где n – целое число (колебания происходят в одной фазе), то  , и колебания усиливают друг друга:
, и колебания усиливают друг друга: 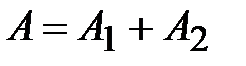 (см.4.20);
(см.4.20);
2) если 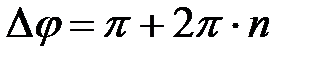 , то
, то 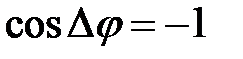 ,
, 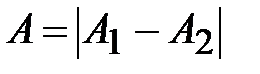 - колебания происходят в противофазе и ослабляют друг друга; а в случае
- колебания происходят в противофазе и ослабляют друг друга; а в случае 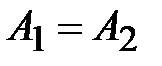 получим
получим 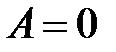 .
.
B. Сложение взаимно перпендикулярных колебаний одинаковой частоты
Складываем два колебания одинаковой частоты, происходящие вдоль осей OX и OY:
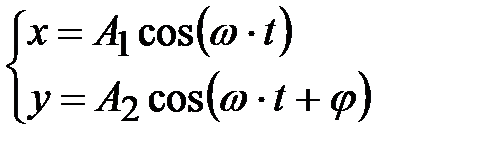
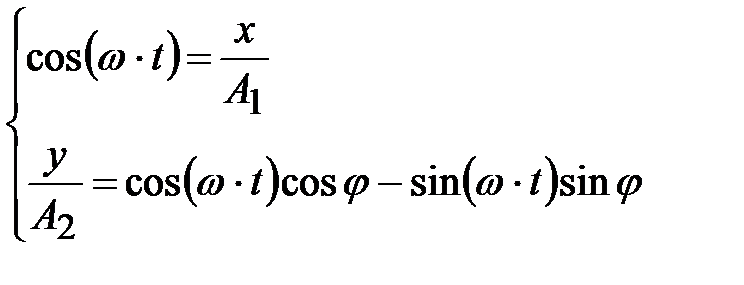
Тогда
 ;
;
после возведения в квадрат и преобразований:
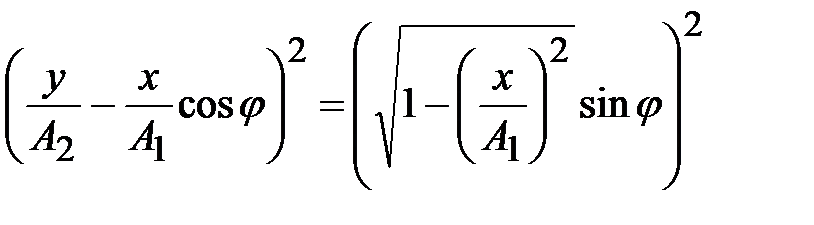 ;
;
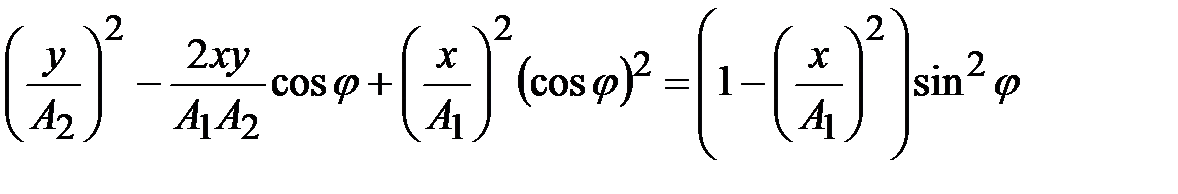 ;
;
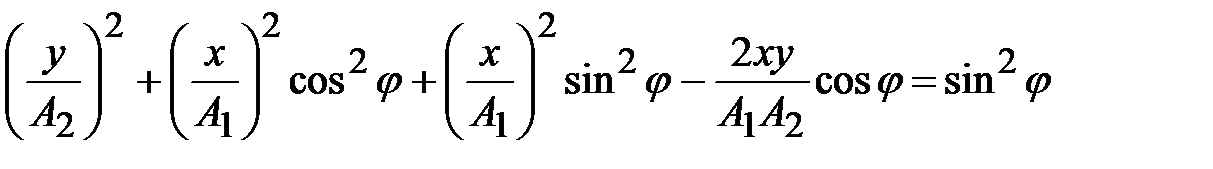 ;
;
 . (4.21)
. (4.21)
В общем случае уравнение (4.21) – это уравнение эллипса (рис.4.9).
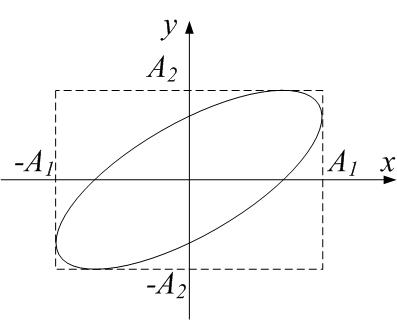
| Рис.4.9 |
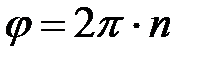
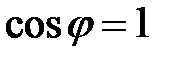 ;
; 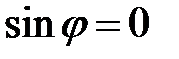
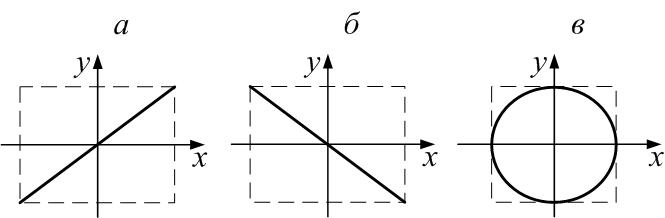
 получим уравнение прямой (точнее, это будет отрезок прямой, поскольку колебания ограничены амплитудой) (рис.4.10а):
получим уравнение прямой (точнее, это будет отрезок прямой, поскольку колебания ограничены амплитудой) (рис.4.10а): 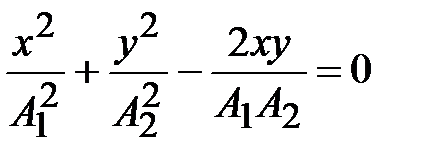

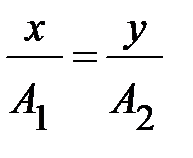
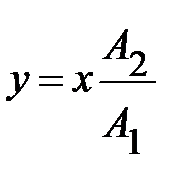 .
.
2) 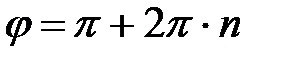
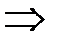
 ;
; 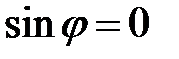
 - прямая (отрезок) на рис.4.10б.
- прямая (отрезок) на рис.4.10б.
3) 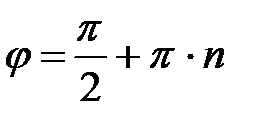
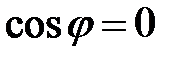 ;
; 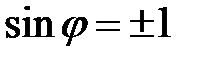 . Потребуем ещё, чтобы
. Потребуем ещё, чтобы 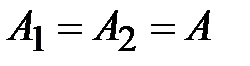 , тогда из (4.21):
, тогда из (4.21):
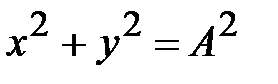 .
.
| Рис.4.10 |
Это – уравнение окружности (рис.4.10в).
С. Сложение взаимно перпендикулярных колебаний кратных частот. Фигуры Лиссажу
Складываются колебания:
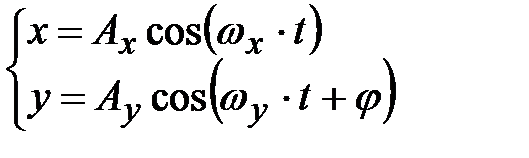
Решение задачи в общем случае очень сложное, поэтому ограничимся примерами. Если частоты относятся как небольшие целые числа:
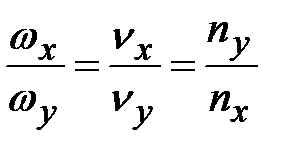 , (4.22)
, (4.22)
то фигура замкнута; условие замкнутости:  .
.
В методе фигур Лиссажу соотношение (4.22) по форме фигуры позволит найти незвестную частоту, если вторая частота известна. Здесь 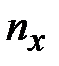 и
и 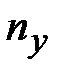 – число точек пересечения фогуры с осями OX и OY (или прямыми, параллельными этим осям) – см. рис.4.11.
– число точек пересечения фогуры с осями OX и OY (или прямыми, параллельными этим осям) – см. рис.4.11.
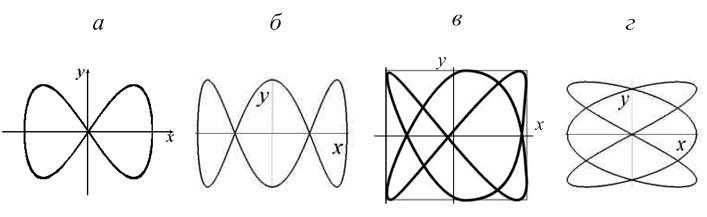
| Рис.4.11 |
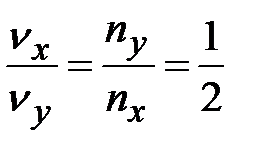 ; б)
; б) 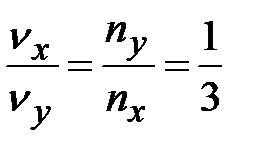 ; в)
; в) 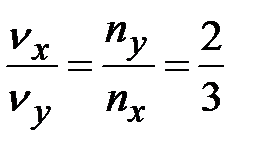 ; г)
; г)  .
.
Круговой процесс (цикл). КПД цикла. Обратимые и необратимые процессы. Второе начало термодинамики по Кельвину и Клаузиусу.
 2018-02-14
2018-02-14 1008
1008
