Задача 1. Однородная балка весом Р=200Н шарнирно закреплена в точке А. К концу балки В прикреплена нить перпендикулярно к балке и переброшена через блок С. Какой груз весом Q необходимо подвесить к нити для того, чтобы балка была в равновесии под углом в 30° к горизонту? Найти так же реакцию шарнира А. Весом нити и трением на блоке С пренебречь (рис. 14а).
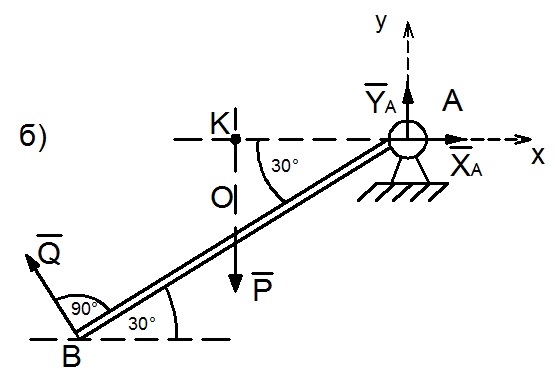
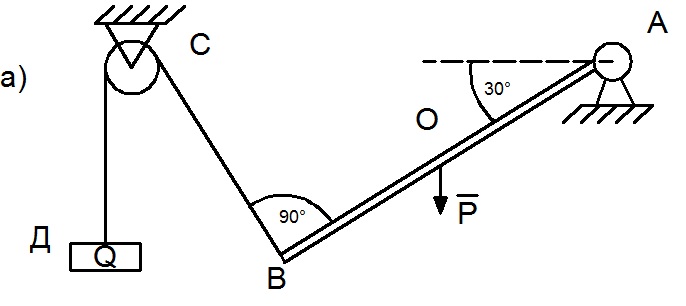
Рис. 14
Решение. 1. Рассмотрим равновесие балки АВ.
2. К балке приложена одна активная сила  , направленная вертикально вниз и приложенная к середине балки в точке О.
, направленная вертикально вниз и приложенная к середине балки в точке О.
3. На балку наложены две связи: нить ВС и неподвижный шарнир в точке А. Освободим балку от связей и покажем на рисунке реакции этих связей. Реакцию неподвижного шарнира представляем ее составляющими 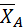 и
и 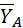 . Так как весом нити и трением на блоке С пренебрегаем, то реакция нити приложена к балке в точке В, направлена по нити и численно равна весу груза (рис 14 б).
. Так как весом нити и трением на блоке С пренебрегаем, то реакция нити приложена к балке в точке В, направлена по нити и численно равна весу груза (рис 14 б).
Таким образом, если балка удерживается в равновесии грузом, переброшенным через неподвижный блок, то нужно отбросить и блок и груз, а их действие заменить реакцией нити, приложенной к балке в точке В и численно раной весу груза 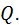
4. Проводим оси координат. Направим ось X по горизонтали направо, а ось Y по вертикали вверх. Составляющие реакции шарнира А, т.е. 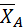 и
и 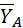 направим параллельно проведенным осям координат (рис. 14 б).
направим параллельно проведенным осям координат (рис. 14 б).
Вычисляем проекции всех сил на оси координат и их моменты относительно точки А (табл. 1).
Таблица 1
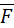 | 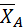 | 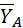 |  | 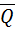 |
 | 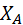 | 0 | 0 | -Q·cos60° |
 | 0 |  | -P | Q·cos30° |
 | 0 | 0 | P·AK | -Q·AB |
5. Запишем уравнения равновесия:
а) сумма проекций всех сил действующих на балку на ось X:
 ,
,  ;
;
б) сумма проекций всех сил на ось Y:
 ,
,  ;
;
в) сумма моментов сил относительно точки А:
 ,
,  .
.
6. Решаем полученную систему уравнений.
Так как  ,
,  , то подставляя числовые значения в уравнение моментов, найдем
, то подставляя числовые значения в уравнение моментов, найдем  .
.
Тогда из первого и второго уравнения получаем, что
 ;
;  .
.
7. Для проверки правильности решения составим уравнение:
 .
.
Подставляя значения входящих величин, получим:
 ,
,
 ,
,
 , 0 = 0. Решение верно.
, 0 = 0. Решение верно.
Задача 2. Однородный стержень АС весом Р=20Н в точке А закреплен шарнирно, а в точке В свободно опирается на опору В. На стержень действует пара сил, момент которой  , а к концу стержня в точке С прикреплена нить, перекинутая через блок Д, к концу которой подвешен груз
, а к концу стержня в точке С прикреплена нить, перекинутая через блок Д, к концу которой подвешен груз  . Найти реакции шарнира А и опоры В, если
. Найти реакции шарнира А и опоры В, если  (Рис. 15).
(Рис. 15).

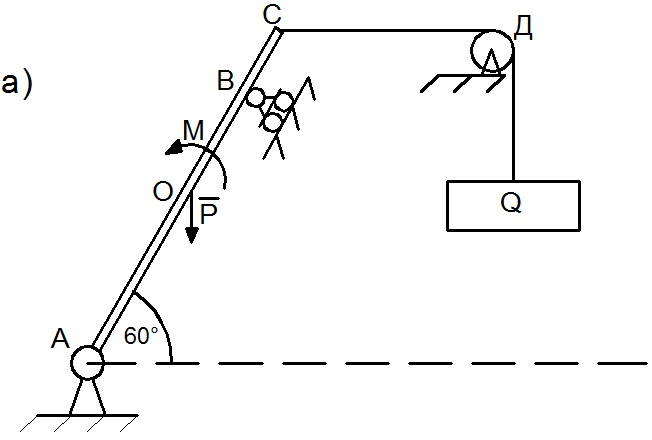
Рис. 15
Решение. 1. Рассмотрим равновесие стержня АС.
2. На стержень действуют сила  , приложенная в точке О и направленная вертикально вниз, а так же пара сил с моментом М (рис. 15б).
, приложенная в точке О и направленная вертикально вниз, а так же пара сил с моментом М (рис. 15б).
3. Начало координат выберем в точке А, укажем оси координат (рис.15б).
4. На стержень наложены следующие связи: неподвижный шарнир в точке А, подвижная опора В и нить CД. Освободим стержень от связей и покажем на рисунке реакции этих связей. Реакцию шарнира А изобразим силами 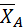 ,
, 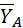 , направленными параллельно осям координат. Реакция подвижного шарнира В
, направленными параллельно осям координат. Реакция подвижного шарнира В 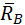 направлена перпендикулярно плоскости, на которой установлена опора. Освободим стержень от нити СД, вдоль нити покажем ее реакцию
направлена перпендикулярно плоскости, на которой установлена опора. Освободим стержень от нити СД, вдоль нити покажем ее реакцию  , причем численно T=Q (рис. 15 б).
, причем численно T=Q (рис. 15 б).
5. Вычислим проекции всех сил на осиxиy, а также моменты этих сил относительно точки А (табл. 2).
Таблица 2
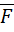 |  |  |  |  |  | M |
 |  | 0 | 0 |  | Q | - |
 | 0 |  | -P |  | 0 | - |
 | 0 | 0 |  |  | 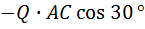 | M |
6. Запишем уравнения равновесия: два уравнения проекций сил на оси координат и уравнение моментов этих сил относительно точки А:
 ,
, 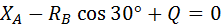 ;
;
 ,
,  ;
;
 ,
,  .
.
7. Решим полученную систему уравнений:
Из последнего уравнения найдем  .
.
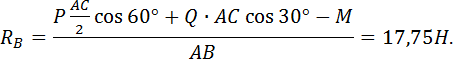
Тогда  .
.

8. Для проверки правильности решения задачи составим уравнение:  .
.
 .
.
Подставляя в это уравнение численные значения входящих величин, имеем:

 ; 0=0, решение верно.
; 0=0, решение верно.
Задача 3. К однородной горизонтальной балке АВ весом Р=200кН, заделанной концом А в стену, приложена пара сил, момент которой М=200кНм. В точке В под углом 60° к горизонту приложена сила F=100кН. На участке ВС действует равномерно распределенная нагрузка интенсивности  . Найти реакцию заделки А, если АВ=4м, ВС=1м (рис. 16а).
. Найти реакцию заделки А, если АВ=4м, ВС=1м (рис. 16а).


Рис. 16
Решение. 1. Рассмотрим равновесие балки АВ.
2. К балке приложены активные силы:  -сила тяжести балки, сила
-сила тяжести балки, сила 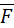 , приложенная в точке В, и пара сил с моментом М. Также на участке балки ВС приложена равномерно распределенная нагрузка интенсивности
, приложенная в точке В, и пара сил с моментом М. Также на участке балки ВС приложена равномерно распределенная нагрузка интенсивности  . Заменим эту нагрузку силой
. Заменим эту нагрузку силой 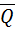 , модуль которой равен
, модуль которой равен 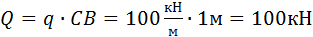 .
.
Точка приложения силы 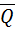 находится в середине отрезка ВС, т.е. ВК=КС=0,5м.
находится в середине отрезка ВС, т.е. ВК=КС=0,5м.
3. На балку наложена одна связь – жесткая заделка в точке А. Эта связь не допускает никаких перемещений, а также любых поворотов балки. Реакциями жесткого защемления являются две силы 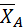 ,
, 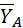 , приложенные в точке А, и пара сил с моментом
, приложенные в точке А, и пара сил с моментом 
(рис. 16 б).
4. Проводим оси координат и вычисляем проекции сил на оси координат и моменты этих сил относительно точки А (табл. 3).
Таблица 3
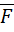 |  |  |  |  | 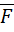 | M |  |
 |  | 0 | 0 | 0 |  | - | - |
 | 0 |  |  | -Q |  | - | - |
 | 0 | 0 |  |  |  | -M |  |
При вычислении момента силы 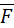 воспользуемся теоремой Вариньона. Силу
воспользуемся теоремой Вариньона. Силу 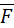 представили двумя ее составляющими, направленными параллельно осям координат и равными
представили двумя ее составляющими, направленными параллельно осям координат и равными  ,
, 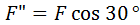 . Тогда, согласно теореме,
. Тогда, согласно теореме,  , где
, где 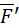 направлена параллельно оси X, а
направлена параллельно оси X, а 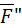 ей перпендикулярна.
ей перпендикулярна.  , так как линия действия этой силы проходит через точку А, а
, так как линия действия этой силы проходит через точку А, а  .
.
5. Запишем уравнения равновесия:
 ;
;
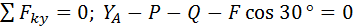 ;
;
 .
.
6. Решаем полученную систему уравнений:
Из первого уравнения: 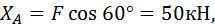
Из второго уравнения: 
Момент в заделке А вычислим из третьего уравнения:

7. Для проверки правильности решения задачи составим уравнение 
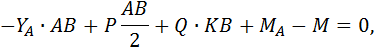

 0 = 0. Решение верно.
0 = 0. Решение верно.

 Задача 4. Балка AД закреплена при помощи неподвижного цилиндрического шарнира А и стержневой опоры
Задача 4. Балка AД закреплена при помощи неподвижного цилиндрического шарнира А и стержневой опоры  . На балку действуют две силы
. На балку действуют две силы  , приложенные в точках B и Д, направленные под углом
, приложенные в точках B и Д, направленные под углом  к балке и равные Р=10 кН. На участке ВС приложена равномерно распределенная нагрузка интенсивности q=2 кН/м. Кроме того, на балку действует пара сил, которая стремится повернуть балку против часовой стрелки, момент этой пары сил равен
к балке и равные Р=10 кН. На участке ВС приложена равномерно распределенная нагрузка интенсивности q=2 кН/м. Кроме того, на балку действует пара сил, которая стремится повернуть балку против часовой стрелки, момент этой пары сил равен  . Определить реакции опор (рис. 17а).
. Определить реакции опор (рис. 17а).
Рис. 17
Решение. 1. Рассмотрим равновесие балки AД.
2. Изобразим на рисунке заданные силы: силы  , приложенные в точках B и Д, силу
, приложенные в точках B и Д, силу 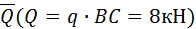 , приложенную в середине отрезка BC, и пару сил с моментом М. Балка закреплена при помощи шарнирно неподвижной опоры А и стержневой опоры
, приложенную в середине отрезка BC, и пару сил с моментом М. Балка закреплена при помощи шарнирно неподвижной опоры А и стержневой опоры  , являющиеся связями для балки.
, являющиеся связями для балки.
3. Отбросим связи и заменим их действие реакциями. Реакция шарнирно неподвижной опоры А приложена в центре шарнира, ее направление зависит от действующих на балку сил и заранее не известна. Поэтому покажем реакцию шарнирно неподвижной опоры А двумя ее составляющими 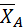 ,
, 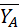 , направленными параллельно осям координат. Реакцию стержневой опоры С направим вдоль стержня от балки к точке закрепления, предположив при этом, что стержень растянут (рис. 17 б).
, направленными параллельно осям координат. Реакцию стержневой опоры С направим вдоль стержня от балки к точке закрепления, предположив при этом, что стержень растянут (рис. 17 б).
4. Проведем оси координат: ось Ax– вдоль балки, Ay – перпендикулярно ей. Вычислим проекции сил  ,
,  , действующих на балку и моменты этих сил относительно точки А (табл. 4).
, действующих на балку и моменты этих сил относительно точки А (табл. 4).
Таблица 4
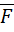 |  |  |  |  |  |  | M |
 |  | 0 | 0 |  |  | 0 | - |
 | 0 |  | -S |  |  | -Q | - |
 | 0 | 0 |  |  |  |  | M |
5. Составим уравнения равновесия.
 ;
;
 ;
;
 ;
;
Момент пары входит только в уравнение моментов с положительным знаком, так как по условию задачи пара сил стремится вращать балку против часовой стрелки.
6. Решим полученную систему алгебраических уравнений.
Из первого уравнения имеем:  .
.
Из третьего уравнения:  .
.
Из второго уравнения:  .
.
Отрицательное значение реакции 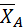 означает, что она направлена в сторону, противоположную указанной на расчетной схеме (рис.17б).
означает, что она направлена в сторону, противоположную указанной на расчетной схеме (рис.17б).
Отрицательное значение реакции стержня  указывает, что стержень сжат.
указывает, что стержень сжат.
7. Проверка. Для проверки решения задачи составим уравнение моментов всех сил, действующих на балку, относительно точки Д:
 .
.
Подставляя в это уравнение значения всех входящих величин, получим:
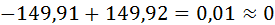 . Таким образом, задача решена верно.
. Таким образом, задача решена верно.
 Задача5. Плита АВ веса P=100Н свободно опирается в точке А на гладкую плоскость и удерживается под углом 45° к горизонту двумя стержнями BC и BД. Треугольник BCД – равносторонний. Точки C и Д лежат на вертикальной прямой. Стержни соединены с балкой и вертикальной стеной шарнирами B, C и Д. Пренебрегая весом стержней найти реакцию опоры А и усилия в стержнях (рис.
Задача5. Плита АВ веса P=100Н свободно опирается в точке А на гладкую плоскость и удерживается под углом 45° к горизонту двумя стержнями BC и BД. Треугольник BCД – равносторонний. Точки C и Д лежат на вертикальной прямой. Стержни соединены с балкой и вертикальной стеной шарнирами B, C и Д. Пренебрегая весом стержней найти реакцию опоры А и усилия в стержнях (рис.  18а).
18а).
Рис. 18
Решение.
1. Рассмотрим равновесие плиты АВ.
2. В центре тяжести плиты, в точке О, приложена активная сила  – вес плиты, направленная вертикально вниз.
– вес плиты, направленная вертикально вниз.
3. Плита, удерживается в равновесии при помощи двух стержней BC и BД и опирается на гладкую поверхность в точке А.
Освободим плиту от связей. Реакция гладкой поверхности  направлена по нормали к поверхности. Реакции стержней BC и BД приложены в точке В плиты и направлены по этим стержням. Считаем, что оба стержня растянуты, поэтому их реакции направляем к точкам закрепления стержней С и Д (рис. 18 б).
направлена по нормали к поверхности. Реакции стержней BC и BД приложены в точке В плиты и направлены по этим стержням. Считаем, что оба стержня растянуты, поэтому их реакции направляем к точкам закрепления стержней С и Д (рис. 18 б).
4. Проведем оси координат и вычислим проекции всех сил, действующих на плиту, на эти оси координат, а также моменты этих сил относительно точки В (табл. 5).
Таблица 5
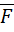 |  |  |  |  |
 | 0 |  | 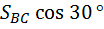 |  |
 | -P |  |  |  |
 |  |  | 0 | 0 |
5. Запишем уравнения равновесия:
 ,
,  ;
;
 ,
,  ;
;
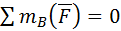 ;
; 
6. Решим полученную систему уравнений:

 .
.
Знак минус у реакции стержня BД означает, что этот стержень сжат.
7. Проверку полученного решения проведем путем составления уравнения  .
.
 ;
;
 ;
;
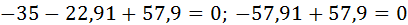 ; 0=0. Решение верно.
; 0=0. Решение верно.
 2018-02-14
2018-02-14 7687
7687
