По принципу максимального правдоподобия за оценку неизвестных параметров принимают такое значение, которое представляется наиболее вероятным на основании опытных данных [12,35].
Пусть 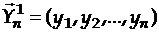 - случайные величины, имеющие какое-то распределение,
- случайные величины, имеющие какое-то распределение, 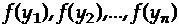 - плотность распределения.
- плотность распределения.
Поскольку источником распределения случайных величин 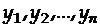 является наличие случайной величины
является наличие случайной величины 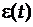 , то законы распределения
, то законы распределения 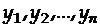 совпадают с законом распределения
совпадают с законом распределения 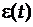 .
.
Параметры распределения разные, причем математическое ожидание разное, а дисперсии при стационарном случайном процессе 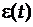 одинаковы.
одинаковы.
Зная плотности распределения, можно вычислить функцию правдоподобия:

В частном случае, если измерения независимы, 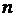 -мерная плотность распределения равна произведению
-мерная плотность распределения равна произведению 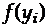 .
.
Функция правдоподобия зависит от неизвестных параметров.
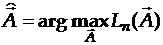 - это оценка максимального правдоподобия.
- это оценка максимального правдоподобия.
Оценка максимального правдоподобия максимизирует нашу функцию.
Согласно принципу максимального правдоподобия за оценку параметров принимают значение, при которых функция правдоподобия достигает максимума.
Для упрощения вычислений обычно максимизируют не исходную функцию правдоподобия, а логарифмическую функцию правдоподобия:
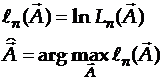 .
.
 2018-02-14
2018-02-14 902
902








