Аналитические методы выравнивания

Аналитические методы выравнивания предполагают наличие тенденции на протяжении всего временного ряда. Выявить тенденцию изменений временного ряда - значит установить, ка­кая математическая функция наиболее пригодна для описания изучаемого нами явления. А зная это, можно рассчитать с той или иной степенью точности уровень интересующего нас показателя в нужный момент.

Следует сразу, же отметить, что применение математических моделей для прогнозирования имеет смысл толь­ко тогда, когда исследователь может на основе теоретического ана­лиза «предугадать» тенденции развития и длительность их сущест­вования. Ведь сами тенденции тоже подвергаются изменениям [24].

Итак, применение аналитических методов выравнивания сводится к построению кривой роста – функции, аппроксимирующей временной ряд, отображающей зависимость исследуемого показателя от времени. Построение кривой роста включает два этапа: идентификация, т.е. определение вида аппроксимирующей математической функции, и определение коэффициентов кривой роста, например, методом наименьших квадратов. Параметры подобранной кривой остаются неизменными для всей известной части ряда.

Следует отметить, что выбор конкретного типа кривой роста должен учитывать характер аппроксимируемого временного ряда и быть обоснованным. Особенно это актуально при исследовании социально-экономических процессов, в которых, как известно, нерегулярная составляющая может быть значительной. Так, применение сложных математических функций (например, полиномов высоких порядков) увеличивает точность модели, но при этом не достигается нужная степень выравнивания, может быть неадекватно описан исследуемый процесс.

Из всего множества всевозможных математических функций обычно используют сравнительно небольшое их число. Это объясняется реально существующими типами изменений, с которыми приходится сталкиваться исследователю [11,34,44,45].

Полиномиальные модели. В общем случае эти модели имеют вид:

.

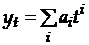В зависимости от диапазона изменения  получаем различные модели.

При 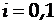 имеем линейную модель. Она описывается уравнением вида

,

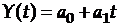где 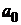- показатель в начальный момент, - прирост за единицу времени.

Для этого типа динамики временных рядов характерно изменение исследуемого показателя за каждый период на одну и ту же величину. Линейная модель является полиномиальной моделью первого порядка.

Если 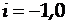, то модель – гиперболическая:

.

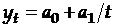При 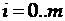 имеем полином степени .

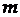Экспоненциальные модели. В общем случае этот вид моделей может быть представлен следующим образом:

.

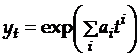При 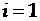 приходим к общеизвестной модели экспоненциального роста первого порядка:

,

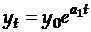где 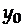— начальный уровень,  - средний темп роста.

Экспоненциальный рост предполагает относительно постоянное и быстрое возрас­тание уровня изучаемого явления, т.е. изменения с постоянным темпом прироста или по сложным процентам, по геометрической прогрес­сии.

Необычайно широкое применение модели экспоненциального роста объясняется чаще всего природой процесса воспроизводст­ва. Под воспроизводством понимается процесс, при котором биологические и социальные системы (или элементы систем) воспроизводят подобные себе. Очевидно, что объем воспроизводства зависит от исходного уровня: чем больше начальное число элементов, способных к воспроизводству, тем больший будет прирост новых элементов.

Некоторые процессы действительно в течение относительно длительного периода изменяются с более или менее постоянными темпами, и в этих условиях такая простая операция, как экстра­поляция существующих темпов на будущее, позволяет получить не такой уж плохой прогноз. И не случайно методом экстраполяции по экспоненте пользуются необычайно широко.

Но у экспоненциальной модели есть свои недостатки. В большинстве случаев для реального процесса характерны изменяющиеся темпы роста, экспоненциальный рост должен рано или поздно столкнуться с ограничениями внешней среды.

S-образные модели. К этому классу относят логистическую модель и кривую Гомперца.

Как видно из графика, логистиче­ская модель предполагает, что снача­ла происходит рост с увеличивающи­мися абсолютными приростами, затем после точки перегиба он замедляет­ся, и процесс постепенно прибли­жается к пределу, т. е. некоторой постоянной величине. Математиче­ская модель логистического роста вы­глядит следующим образом:

,

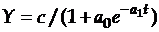где 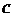 - предел роста;  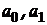- параметры процесса, причем первый параметр характеризует положение кривой на оси времени, а второй – крутизну кривой.

Кривая Гомперца сходна с логистой и описывается уравнением:

.

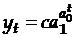Параметры модели имеют тот же смысл, что и у логистической кривой.