Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. В модели авторегрессии 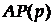 порядка
порядка 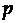 текущий уровень ряда представляется в виде взвешенной суммы
текущий уровень ряда представляется в виде взвешенной суммы 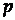 предыдущих наблюдений:
предыдущих наблюдений:
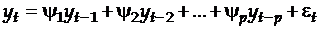 .
.
Или
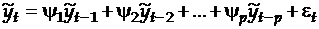 , где
, где 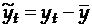 .
.
Порядок авторегрессии определяется путем перебора, а его начальное значение определяется на основе анализа АКФ и ЧАКФ. Лучшей считается величина, при которой достигнута наименьшая дисперсия ошибок.
В сезонной модели авторегрессии порядок выбирается равным периоду сезонности. Модель авторегрессии целесообразно использовать для стационарных рядов.
Введем оператор сдвига назад:
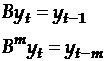
Тогда модель 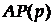 можно записать как:
можно записать как:
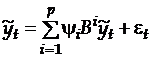 .
.
Введем авторегрессионный оператор порядка 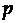 :
:
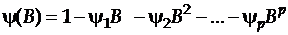
Тогда модель запишется в виде формулы
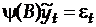 .
.
Одним из видов авторегрессионных процессов является марковские процессы. Марковскими называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только состоянием в настоящий момент, и не зависит от того, каким путем объект достиг этого состояния. В терминах корреляционного анализа для временных рядов марковский процесс можно описать следующим образом: существует статистически значимая корреляционная связь исходного ряда с рядом сдвинутым на один временной интервал, и отсутствует c рядами, сдвинутыми на два, три и т. д. временных интервала. В идеальном случае эти коэффициенты корреляции равны нулю.
С помощью уравнения авторегрессии такой ряд описывается следующим образом:
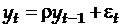 ,
,
где 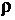 - коэффициент автокорреляции с лагом 1:
- коэффициент автокорреляции с лагом 1:
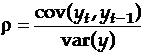 .
.
Кроме марковских процессов из авторегрессионных часто встречающимися являются так называемые процессы Юла, в которых учитывается авторегрессия не только первого, но и второго порядка:
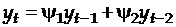 ,
,
где 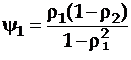 ,
, 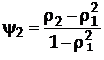 ,
,
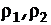 - коэффициенты автокорреляции с лагами 1 и 2 соответственно.
- коэффициенты автокорреляции с лагами 1 и 2 соответственно.
 2018-02-14
2018-02-14 758
758








