Это наиболее распространенная форма описания входного потока, позволяющая достаточно просто исследовать СМО аналитически. В нем события происходят в непредсказуемые (случайные) моменты времени. Промежутки времени между событиями также являются случайными.
Рассматриваемый поток можно определить как поток, в котором число требований, поступающих в заданном временном интервале времени τ, распределено по закону Пуассона с параметром a=λ∙τ, где λ - интенсивность потока, т.е. среднее число требований, поступающих в единицу времени, а вероятность, что на интервале τ возникнет ровно k требований, равна
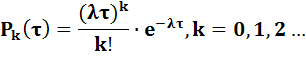
Согласно свойству закона Пуассона величина 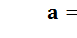 есть математическое ожидание (среднее значение) и дисперсия числа требований, поступающих на интервале времени
есть математическое ожидание (среднее значение) и дисперсия числа требований, поступающих на интервале времени 
Величина  - (интенсивность потока требований) - одна из основных характеристик потока равна математическому ожиданию числа требований, поступающих в единицу времени.
- (интенсивность потока требований) - одна из основных характеристик потока равна математическому ожиданию числа требований, поступающих в единицу времени.
Простейший Пуассоновский поток обладает свойствами стационарности, ординарности и отсутствия последействия.
Стационарность означает, что статистические характеристики потока (распределение числа требований в единицу времени, распределение интервала между соседними требованиями) во времени не меняются.
Ординарность означает практическую невозможность одновременного появления двух и более требований. Т.е. вероятность появления двух и более требований на интервале ∆t→0 бесконечно мала по сравнению с вероятностью появления одного требования
Отсутствие последействия означает, что вероятность появления k требований на интервале [t, t+τ] не зависит от числа требований, появившихся до момента t и положения интервала τ на временной оси.
Найдем закон распределения интервала времени между двумя соседними требованиями для простейшего Пуассоновского потока.
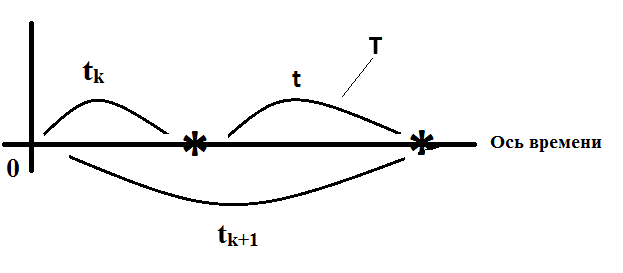
Пусть T – случайная величина – интервал между требованиями.
Вероятность того, что величина T примет значение больше или равно t равна вероятности того, что на интервале продолжительностью t не возникнет ни одного требования, т.е.
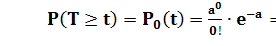 , где
, где 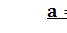 .
.
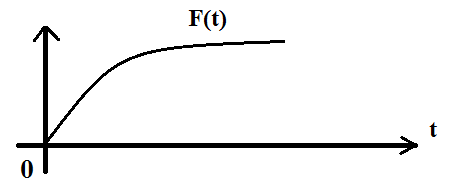
Отсюда Функция распределения длины интервала между требованиями, имеет вид
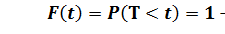 при
при  .
.
Функция плотности распределения будет
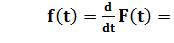 при t при t  |
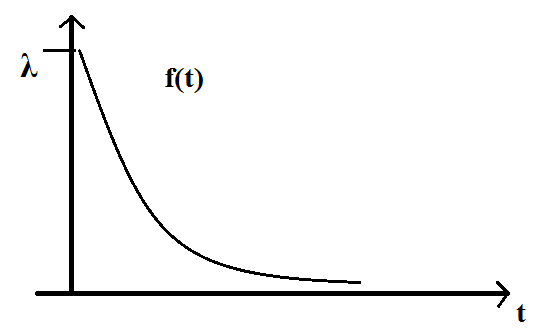
Как видим это экспоненциальный закон распределения. Его основные числовые характеристики:
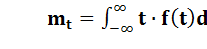 ,
, 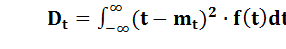
Как видно из выражения для функции распределения, вид закона распределения не зависит от положения интервала между требованиями на временной оси (стационарность) и от того, появились или нет требования раньше (отсутствие последействия). Т.е. е сли промежуток времени, распределенный по экспоненциальному закону уже длился некоторое время  , то это никак не влияет на закон распределения оставшейся части промежутка - он будет таким же, как и закон распределения всего промежутка T. Этим свойством обладает только экспоненциальный закон. Для него можно показать, также, и выполнение условия ординарности.
, то это никак не влияет на закон распределения оставшейся части промежутка - он будет таким же, как и закон распределения всего промежутка T. Этим свойством обладает только экспоненциальный закон. Для него можно показать, также, и выполнение условия ординарности.
При анализе реальных входных потоков оказывается, что простейший поток имеет широкое распространение на практике. Это обуславливается предельными свойствами, согласно которым простейший поток возникает при суммировании большого числа взаимно независимых потоков малой интенсивности, обладающих свойствами стационарности и ординарности, при этом свойство отсутствия последействия для них (по отдельности) может и не выполняться.
 2018-02-13
2018-02-13 2204
2204
