Другие виды входных потоков

Нестационарный Пуассоновский поток. Если поток событий ординарный, без последействия, но с переменной плотностью числа событий, приходящихся на единицу времени 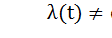, то такой поток событий называется нестационарным Пуассоновским.

Для него число требований, поступающих на участке времени длиной , начинающемся в точке  так же подчинено закону Пуассона

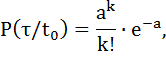
но значение параметра   зависит и от  и от

 

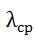
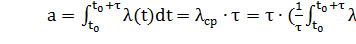
Как видим, закон распределения интервала времени между двумя соседними требованиями отличается от экспоненциального и зависит от вида функции.

Неординарный Пуассоновский поток. Сохраним стационарность и отсутствие последействия, но откажемся от ординарности следующим образом: Моменты прихода требований составляют простейший Пуассоновский поток, но в каждый из этих моментовt_i может придти группа из m требований, причем m случайно и задается распределением P(m) – вероятностью того, что в группе будет m требований. Тогда вероятность прихода в случайный момент (t_i) j требований равна:

P =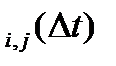

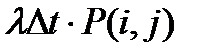
Поток с ограниченным последействием. Рассмотрим ординарный поток событий.

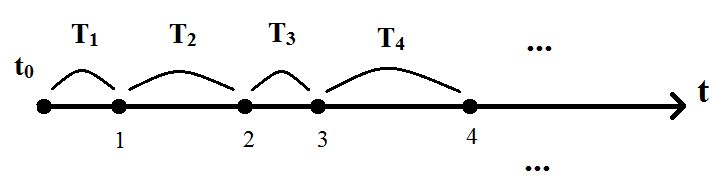
Здесь 1,2,3,… события, T₁, T₂ ,… интервалы времени между событиями.

Если интервалы времени между последовательными событиями представляют собой независимые случайные  величины, то такой поток событий называется потоком с ограниченным последействием (поток Пальма).

Потоком Пальма является поток отказов элементов в техническом устройстве, если отказы наступают независимо, а отказавший элемент мгновенно заменяется новым. Поток отказов часто называют потоком восстановлений т.к. в момент отказа происходит мгновенное восстановление элемента. Потоком с ограниченным последствием является, также, поток не обслуженных заявок, покидающих систему (Теорема Пальма: если на вход СМО поступает поток заявок типа Пальма и в случае занятости каналов обслуживания заявка покидает систему не обслуженной (получает отказ), а время обслуживания заявок в системе подчинено экспоненциальному закону, то поток не обслуженных заявок также является потоком Пальма.).

Частным случаем потока Пальма является простейший поток.

Другим частным случаем потоков Пальма являются потоки Эрланга, которые образуются «просеиванием» простейшего потока.

Поток Эрланга: если из простейшего потока будем удалять требования через одно, то оставшиеся требования образуют поток Эрланга первого порядка, если будем удалять требования парами, оставляя каждое третье, то они образуют поток Эрланга второго порядка и т.п. Если из простейшего потока будем удалять требования группами по k штук в каждой группе, то оставшиеся требования образуют поток Эрланга k –го порядка (см. рис).

 

_*____*____*____*____*____*____*____*____*_____*__ Простейший поток

_*_________*_________*_________*_________*________ Поток Эрланга 1-го порядка

_*______________*______________*_______________*___ Поток Эрланга 2-го порядка

_*___________________*___________________*__________ Поток Эрланга 3-го порядка

 

Интервал времени между требованиями в потоке Эрланга К-го порядка подчинён закону распределения Эрланга К-го порядка как закон распределения суммы (К+1) независимых случайных величин с экспоненциальным законом распределения

f_к(t) 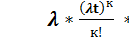₌ при 

с параметрами:

m_к=(к+1)_*m₀ = (к+1)*                       - мат. Ожидания;

D_К  = (К+1)*D₀ = (К+1)*       - дисперсия,

где: m₀,D₀ - параметры экспоненциального закона (закон Эрланг нулевого порядка).

    Можно показать, что при увеличении порядка (K) поток Эрланга становится все более регулярным.

Рассмотрим в качестве характеристики «меры случайности» коэффициент вариацииV_T=Ϭ_T/m_T, который применяется в ТВ для неотрицательных случайных величин.

Для закона распределения Эрланга К-го порядка он будет равен

V_T^(К)=Ϭ_T^(К)/m_T^(К)= =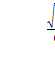

Как видим, по мере увеличения значения Kкоэффициент вариации стремиться к нулю, т.е.величина рассеивания случайной величины относительно среднего уменьшается, т.е. поток становится все более регулярным.

Кроме рассмотренных выше, на практике имеют распространение:

- Неординарные потоки (требования поступают не по одному, а группами);

- Сложные детерминированные потоки – неслучайные по сути, но со сложной функцией моментов поступления.

- Дискретные потоки. В них требования могут поступать только в определённые моменты времени. Например на транспорте – по расписанию и т.д.

 

Время обслуживания

Эффективность функционирования системы обслуживания, как уже говорилось ранее, определяется в частности временем обслуживания каждого требования. Длительность обслуживания в общем случае является случайной величиной, подчинённой некоторому закону распределения. В ТМО наиболее распространены следующие виды законов.

1. Показательное распределение длительности времени обслуживания.В этом случае время нахождения требования в канале обслуживания подчинено экспоненциальному закону распределения с параметром µ – среднее число заявок, обслуженных в канале за единицу времени (интенсивность обслуживания)

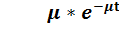g(t) = t .

Мат. ожидание и дисперсия времени обслуживания заявки в канале будут:

m_(t) = ; D_(t) = .

Показательное распределение времени обслуживания целесообразно применять в тех случаях, когда большее число требований требует для своего обслуживания сравнительно малого времени, а меньшее число требований – большого (например на потоке – много мелких отправлений (заявок) – марки, конверты,…. реже заказные письма, телеграммы). Совсем редко отправление одним клиентом сразу большого числа заказной корреспонденции.

Основное достоинство экспоненциального распределения в задачах анализа СМО состоит в том, что оно не обладает памятью (не зависит от начала отсчета), и, следовательно, открывает возможности для построения марковской модели СМО.

2. Эрланговское распределение длительности обслуживания. Используется при анализе СМО в тех случаях, когда процесс обслуживания можно представить как К последовательных, независимых этапов, длительность обслуживания на каждом из которых подчинена экспоненциальному закону распределения с параметром  (распределение Эрланга (К-1)-го порядка).

3. Нормальное распределение. Часто встречаются ситуации, когда время обслуживания хорошо сгруппировано вокруг среднего значения и отклонения от него распределены симметрично с экспоненциально убывающей плотностью на ветвях. В таких случаях напрашивается использование нормального распределения. Однако, применять его надо с осторожностью. Дело в том, что генерация значений времени обслуживания в соответствии с нормальным законом чревата тем, что возможно появление отрицательных чисел, чего ни в коем случае быть не должно. Отрицательных чисел практически не будет, если среднее время обслуживания в 5-6 раз больше, чем С.К.О.

4. Постоянная длительность обслуживания. Применяется для приближённого расчёта СМО с сильной идеализацией процессов обслуживания.

Кроме этих законов распределения могут применяться и другие:

· с нестационарной интенсивностью обслуживания

· с неординарным потоком заявок.

· с зависимостью времени обслуживания от типа требования и др.

В этих случаях получить простые аналитические выражения для анализа СМО часто не представляется возможным. Поэтому:

- либо используют приближённые вычисления, переходя к экспоненциальным законам с эквивалентными характеристиками;

- либо приводят не марковские модели к марковским, используя специальные приемы;

- либо используют для вычислений специальные модели, например имитационные.