Системы с ограниченным временем ожидания

Пусть система имеет n каналов обслуживания. Входящий поток требований – простейший с интенсивностью λ. Время обслуживания распределено по экспоненциальному закону с параметром μ. Если в момент поступления требования все каналы заняты, то оно встает в очередь. Однако время пребывания требования в очереди – ограниченно. По окончанию этого времени, если требование не поступило на обслуживания, то оно покидает систему не обcлуженным.

Следует отметить, что ограничение на время ожидания в очереди носит принципиальный характер, т.к. при вычислении вероятностей состояний СМО необходимо знание не только текущего состояния (числа требований в системе), но и того, как давно пришли требования, ожидающие обслуживания. Таким образом, процесс функционирования системы характеризуется наличием последействия и, в общем случае, перестает быть марковским. При этом максимальное время ожидания может быть как детерминированным, так и случайным.

 

Рассмотрим случай, когда максимальное время ожидания T = const. В этом случае вероятность перехода системы из одного состояния в другое зависит не только от того, сколько требований находится в системе на обслуживании и в очереди (т.е. от состояния системы), но и от того, как давно требование, стоящее в очереди, находится в системе. От этого зависит – будет ли требование оставаться в системе или покидает ее, как только время ожидания превысит допустимое. Т.е. налицо последействие и последовательность состояний системы (процесс изменения состояний) – не марковский.

Для описания процесса функционирования такой СМО нельзя, напрямую, использовать уравнения размножения и гибели. Однако, описание СМО с помощью марковской модели возможно, если использовать расширение понятия состояния. Для того, чтобы прогнозировать распределения состояний в будущем, необходимо знать, как давно пришли в систему требования, которые в настоящее время находятся в очереди. Это можно сделать, включив в число обобщенных координат, описывающих состояние СМО, давность прихода каждого ожидающего требования, или, что то же самое, время, которое осталось у него до окончания срока ожидания. Расширение понятия состояния приводит к увеличению мерности задачи при учете состояний системы. (см. конспект Бомас.)

Для исследования подобных СМО как не марковских (как, впрочем, и любых других, в том числе и марковских) широко используется имитационное моделирование. При этом оценки параметров исследуемой СМО ищутся на основе статистической обработки результатов моделирований, полученных по множеству прогонов (реализаций).

 

Пусть Максимальная длительность ожидания ограниченна случайной величиной. В этом случае все зависит от закона распределения ограничения максимального времени ожидания Ʈ, т.к. именно это ограничение вносит в систему последействие. Поэтому вернуть процессу функционирования СМО марковость крайне просто. Достаточно принять для описания случайной величины Ʈ экспоненциальное распределение. Однако при этом нельзя забывать, что такая операция возможна лишь в том случае, когда реальное распределение или действительно экспоненциальное, или близко к нему. Если это не так, то сформированная математическая модель будет неадекватна реальной СМО.

Ограничимся случаем, когда максимальная длительность ожидания требования в очереди Ʈ имеет экспоненциальное распределение.

 (функция распределения), 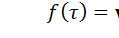 (функция плотности). Здесь ν – параметр закона распределения. Среднее значение  будет  .

Такие процессы функционирования СМО можно представить следующим образом(см. рис.).

На вход системы поступает поток требований (простейший) с интенсивностью . Если не все каналы заняты (k < n), то пришедшие требования сразу же начинают обслуживаться. Обслуженные требования покидают систему с интенсивностью .

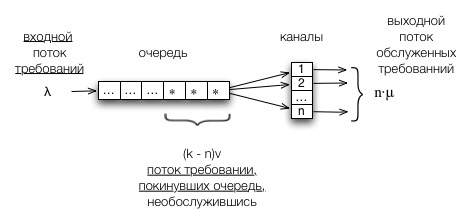
Если все каналы системы заняты, (k > n), то обслуженные требования покидают систему с интенсивностью . Кроме того, возникает еще один поток требований – покидающих систему не дождавшись обслуживания. Интенсивность этого потока равна .

Т.к. показательное распределение максимального времени ожидания также обладает свойством «отсутствия памяти», т.е. распределение оставшегося времени ожидания не зависит от того, сколько времени требование уже прождало в очереди, то последовательность состояний системы оказывается «без последействия» и является «Марковской». Это позволяет описать ее с помощью уравнений «размножения и гибели». В частности, для неограниченной очереди (m = ∞) они имеют вид:

..

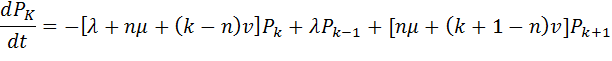
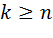
Значения финальных вероятностей соответственно равны:

Из ,  ,

.

Зная значения финальных вероятностей можно найти основные характеристик функционирования СМО в стационарном режиме (m_кан; m_оч; m_отк и другие).

При определении характеристик функционирования СМО необходимо иметь в виду, что не все требования, поступившие в систему, будут обслужены.

1) Вероятность того, что требование, подошедшее к системе, получит отказ

2) Вероятность того, что пришедшее требование поступит в систему.

 .

Поток этих требований с интенсивностью λ_сист=λ·P_сист=λ(1-Р_n+m) разобьётся на два потока:

- обслуженных требований, с интенсивностью λ_обс= m_кан·µ;

- покинувших систему не обслуженными, из-за ограничения на время ожидания в очереди, с интенсивностью λ_пок = m_оч·ν.·

Причем, в стационарном режиме для него будет выполняться условие λ_сист=λ_обс+ λ_пок.

Тогда для любого требования, вошедшего в систему из входного потока, вероятности обслуживания p_обс или не обслуживания (покидания системы не обслуженными p_пок) (в стационарном режиме) будут пропорциональны интенсивностям соответствующих потоков:

,

а для требования, подошедшего на входе к системе, соответствующие вероятности будут равны:

,

Следует отметить, что в режиме статистического равновесия всегда должно выполняться следующее условие равенства потоков требований:

λ = λ_отк + λ_сист= λ_отк + λ_обс+ λ_пок.

 

Средние временные характеристики для требований, на основании формул Литтла будут:

1. Среднее время нахождения в канале обслуживания

2. Среднее время нахождения в очереди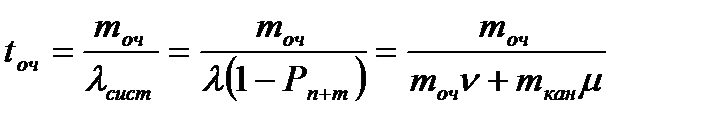

3. Среднее время нахождения в системе

 

 

ЗАМКНУТЫЕ СМО

 

Наряду с задачами, когда интенсивность входного потока требований в систему λ неизменна, на практике часто встречаются задачи, когда число источников требований ограничено, и интенсивность входного потока зависит от того, сколько источников уже послало требования в систему на обслуживание. В качестве примера рассмотрим следующую задачу.

Система содержит R станков, которые обслуживают n рабочих. Каждый станок может отказать в случайный момент времени. Время безотказной работы каждого станка подчинено экспоненциальному закону распределения , где t – момент наступления отказа, λ – параметр, который можно рассматривать как интенсивность потока отказов одного станка, если считать, что после отказа он мгновенно переводится в рабочее состояние и снова работает до очередного отказа.

Если хотя бы один из рабочих свободен, то станок начинает обслуживаться. Время обслуживания распределено также экспоненциально с параметром µ. Если все рабочие заняты, то станок становится в очередь на обслуживание (ремонт), длина которой не может быть больше чем m = R-n.

Схематически данную систему, как СМО можно представить в следующем виде:

 

Заявки (R-k)                                        каналы (n)

                      Очередь (k-n)

m 2 1

                       Входной поток                          выходной

                                                                               поток

                       (R-k) λ                                                            (nµ)   

 

 

    Обозначим k – число заявок на обслуживание (число отказавших станков), 0 ≤ k ≤ R. Тогда интенсивность входного потока заявок зависит от числа отказавших станков и будет равна (R-k)·λ. С учётом этого уравнения Колмогорова-Чепмена, которыми можно описать  данную СМО, примут вид (при условии, что R>n ):

Т. к. общее число состояний системы конечно, то при t в ней существует режим статистического равновесия. Приравняв правые части уравнений нулю можно найти значения финальных вероятностей:

    .

Зная значения финальных вероятностей можно найти основные характеристики работы СМО в стационарном режиме, например:

1) Среднее число отказавших станков

M_отк

2) Среднее число исправных станков

M_испр = R - M_отк

3) Среднее число станков, находящихся в ремонте

M_рем

4) Среднее число неисправных станков, ожидающих ремонта (в очереди)

M_ож.рем

 

Все рассматриваемые выше СМО мы анализировали в предположении, что все потоки событий, происходящих в системе – простейшие. Это позволяло описывать их достаточно просто с помощи уравнений Колмогорова- Чепмена и, в частности, уравнений размножения и гибели. Кроме того – получать достаточно простые выражения для финальных вероятностей состояний системы и её основные характеристик в режиме статистического равновесия.