СМО без ожидания. Уравнения Эрланга

Рассмотрим следующую задачу. Имеется СМО с n каналами обслуживания. На вход системы поступает поток требований(заявок).В случае наличия свободного канала заявка поступает в систему на обслуживание. Если в момент поступления заявки все каналы заняты, то она получает отказ, покидает систему не обслуженной и в дальнейшем обслуживании не участвует. Системы(с отказами) подобного рода называются СМО без ожидания.

Пусть входной поток заявок - простейший с интенсивностью - 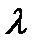 требований в единицу времени.

Время обслуживания заявки T 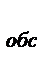 подчинено экспоненциальному закону распределения с параметром 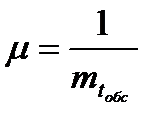.В этом случае параметр 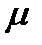можно рассматривать как интенсивность потока обслуживания занятого канала (если он бесперебойно обеспечивается заявками на обслуживание), являющегося простейшим потоком. По классификации Кендалла её можно обозначить как M/M/n с длиной очереди равной нулю.

Составим граф состояний для данной системы.

 

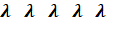
2*       k* (k+1)* n*

 

Здесь состояние 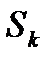 (k = 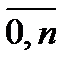) соответствует числу заявок, находящихся в системе на обслуживании и равно числу занятых каналов.

Переход системы из состояния 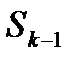 в состояние  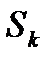происходит при поступлении очередной заявки с интенсивностью 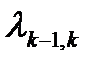= 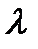, а из состояния 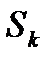в состояние  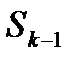- при обслуживании любой из заявок в одном из k каналов системы с интенсивностью .

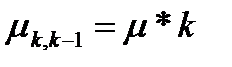Так как оба потока - входной и обслуживание – простейшие, то система является марковской, а процессы, в ней протекающие могут быть описаны как процессы размножения и гибели с помощью уравнений Колмогорова-Чепмена.

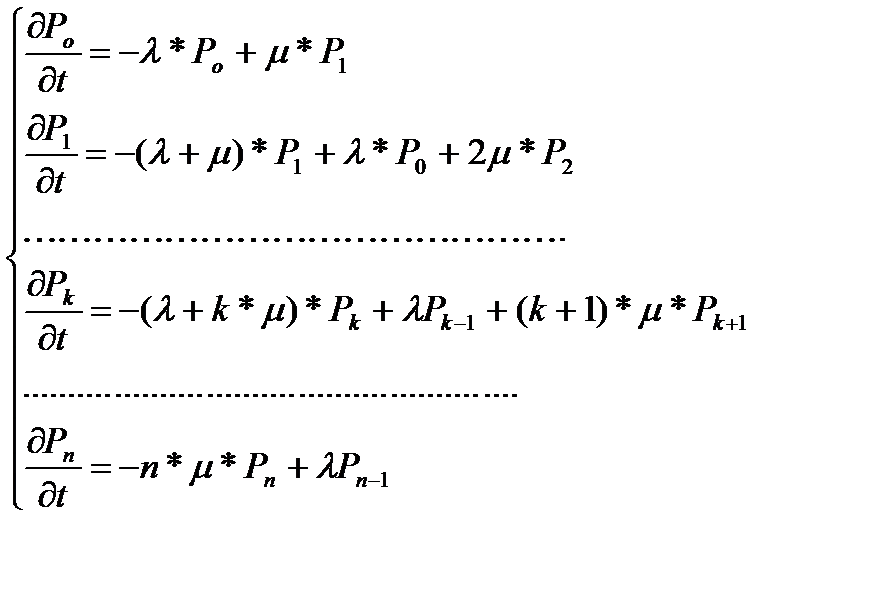
Задав начальные условия и решив данную систему дифференциальных уравнений можно найти все 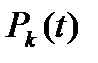 - вероятность того,что в момент времени t в системе находится k требований (занято k каналов обслуживания).

Значения финальных вероятностей найдем, приравняв 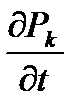= 0 и решив, соответственно, систему алгебраических уравнений.

Используя найденные ранее выражения для финальных вероятностей – получим:

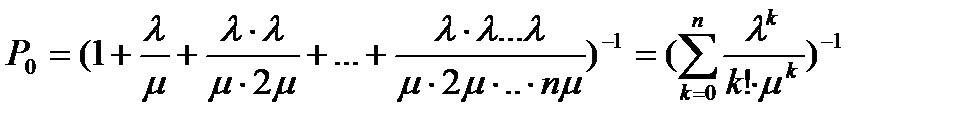
Обозначим 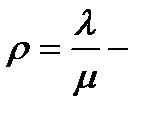приведённая плотность потока заявок. Её можно рассматривать как среднее число требований, приходящихся на среднее время обслуживания одного требования. Тогда

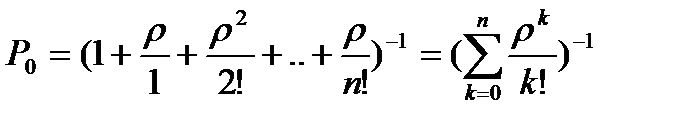
И вероятности состояний, соответственно

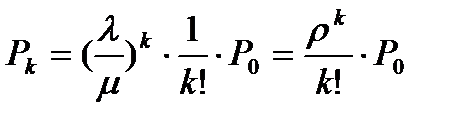
Дифференциальные уравнения, описывающие поведение системы без ожидания называются уравнениями Эрланга, а выражения для финальных вероятностей- формулами Эрланга- в честь основателя ТМО - датского учёного Эрланга, чьи исследования телефонных линий в начале 20-го века, заложили основы современной Теории Массового Обслуживания.

Зная значения финальных вероятностей можно найти основные характеристики работы СМО в стационарном режиме.

1) Вероятность того, что пришедшее требование получит отказ

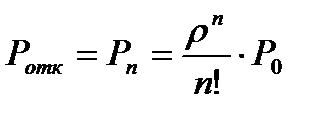
2) Вероятность того, что пришедшее требование будет обслужено

P_обс=1-Р_отк=1-Р_n=1 -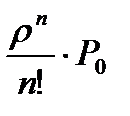

3) Абсолютная (фактическая) пропускная способность системы (среднее число требований, обслуженных за единицу времени)

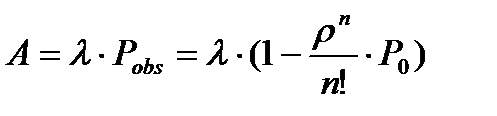
4) Максимальная пропускная способность системы (максимальное среднее число требований, которое может обслужить система за единицу времени, если все каналы будут постоянно заняты)

A_max=n*µ.

5) Среднее число занятых каналов

m_кан =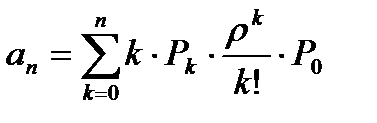

Так как каждый канал в единицу времени из А заявок, обнаруженных системой обслуживает ровно µ, то среднее число занятых каналов может быть найдено как

m_кан=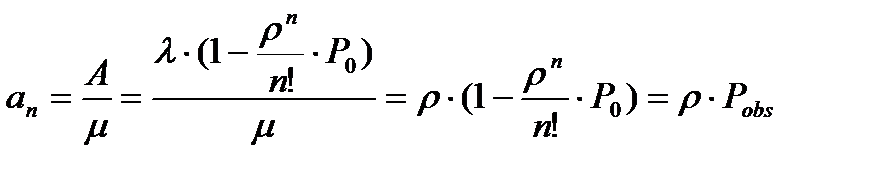

6) Интенсивность потока отказов

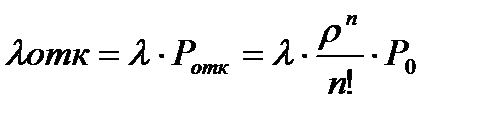
7) Интенсивность потока обслуженных заявок

µ_обс = µ* m_кан= µ* 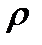*P_обс= λ*P_обс

Как мы знаем, для рассматриваемой СМО, среднее время нахождения заявки в системе равно среднему времени нахождения  заявки в канале обслуживания (очередь отсутствует).t_сист= .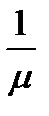 

Аналогично его значение можно получить и по формуле Литтла: t_сист=m_си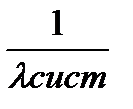ст* m_сист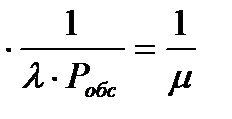

 

СМО С ОЖИДАНИЕМ.

 

Рассмотрим теперь другую задачу. Имеется СМО с n каналами обслуживания. На вход системы поступает поток требований (заявок). В случае наличия свободного канала заявка поступает на обслуживание. Если в момент поступления заявки все каналы заняты, то заявка становится в очередь, ожидая пока освободится какой-либо канал.

Такие системы называются системами с ожиданием. При этом время ожидания в очереди может быть как неограниченным («чистые системы с ожиданием»), так и ограниченным. Кроме того длина очереди может быть как не ограничена, так и ограничена. В случае заполнения всей очереди, пришедшие требования также получают отказ и не обслуживаются.