СМО с ограниченной длиной очереди

Рассмотрим n- канальную СМО с очередью, максимальная длина которой равна m. Время ожидания в очереди – не ограниченно.

Поток требований на входе в систему простейший с интенсивностью . Поток обслуживания также простейший с интенсивностью . В этом случае система будет марковской вида M/M/n/m и изменения вероятностей состояния могут быть описано с помощью уравнений размножения и гибели вида

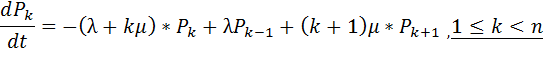
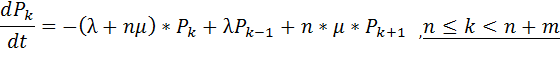
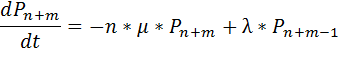
Т.к. число состояний СМО конечно, то в ней существует стационарный режим, и выражения для финальных вероятностей могут быть записаны в следующем виде:

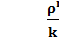= , 1≤k≤n

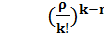= * , n≤k≤n+m,

где , найденная из нормирующего условия 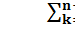=1,будет равна

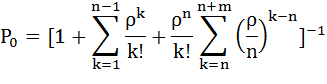
Учитывая, что вторая сумма, как сумма членов геометрической прогрессии равна

, получим окончательно

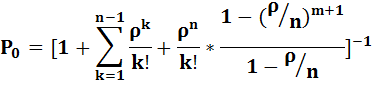
Основные характеристики СМО в стационарном режиме будут:

1) Вероятность того, что пришедшее требование получит отказ

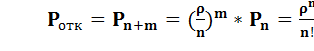2) Вероятность того, что пришедшее требование будет обслужено.

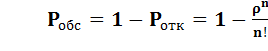3) Абсолютная пропускная способность системы (среднее число требований, обслуженной за единицу времени)

A= *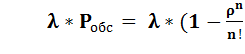

4 ) Вероятность того, что все каналы обслуживания заняты.

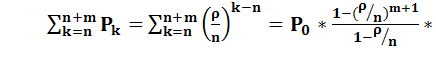
5) Среднее число занятых каналов.

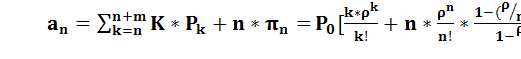= m_кан

Или, иначе, через абсолютную пропускную способность системы:

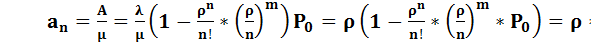= m_кан

6) Средняя длина очереди.

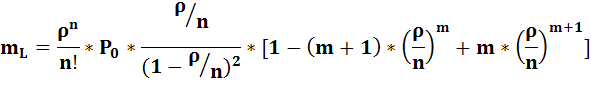
7) Среднее число требований в системе можно найти как

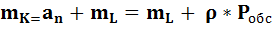
8) Среднее время нахождения требования в очереди

* *

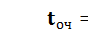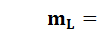9)Общее время нахождения требования в системе будет

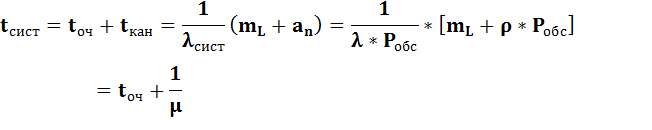
Полученные выражения носят общий характер. Положив в них m=0 получим значения и характеристики СМО для систем без ожидания. Положив m=∞, получим выражения для СМО с неограниченным числом мест в очереди.

Пример. Ателье обслуживает жителей 2-х микрорайонов. Интенсивности заявок с обоих микрорайонов равна 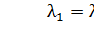чел/час. Среднее время выполнения заявки составляет 20 мин. Число работников в ателье (n) – 2 человека. Определить основные характеристики работы ателье, если:

1)Очереди невозможны(m=0).

2)Очереди не ограничены (м=∞).

3) Как изменится эффективность работы, если каждый из работников будет обслуживать клиентов только одного района.

1) Рассмотрим случай, когда очередь отсутствует (m=0)

а) Каждый работник обслуживает жителей любого района. Тогда:

n=2; 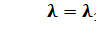=4; µ= ; ;

; ;

* = ; * = ;

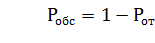= = ; =0,724;

A= * =4* =2,9; ;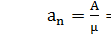

б) Каждый работник обслуживает жителей только одного района. Тогда:

n=1; =2; µ=3; ;

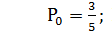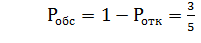
A= * =2*3/5=1,2;

Как видим, во втором случае снижается вероятность обслуживания каждого клиента (с 0,724 до 0,6) и общее число обслуживаемых клиентовА=2*1,2=2,4 (меньше чем2,9). Загрузка мастеров так же падает

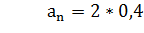(меньше чем 0,96).

2) Рассмотрим случай, когда очередь не ограничена (m=∞)

а) Каждый работник обслуживает жителей любого района. Тогда:

n=2; 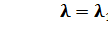=4; µ=3; ;

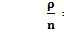< 1 (стационарный режим существует);

= ;

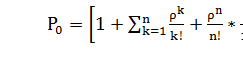* 1≤k≤n; ; ;

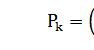* k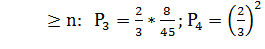

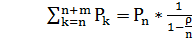
A= * = ;

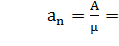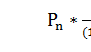= =1,07; *

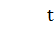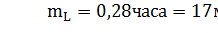
б) Каждый работник обслуживает жителей только одного района. Тогда:

n=1. λ = 2; μ = 3; ρ =

P₀= (1 + ρ)^-1= P_k=P_n· _k>n

P₁ = ρ*P₀ = = , P₂ = ρ*P₁ = = , P₃= = , ……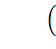

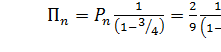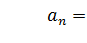
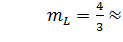
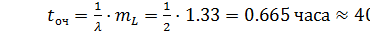
В случае неограниченной очереди (все жители обслужены) при том же среднем числе загруженных каналов 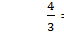увеличивается средняя длина очереди (1.33 в каждом ателье против 1.07 – общая очередь в ателье с 2-мя мастерами). Среднее время ожидания в очереди при этом возросло более чем в 2 раза с 17 мин. до 40 мин.