На вычерченную в принятом масштабе арку надо нанести все заданные размеры и нагрузку. Для заданных сечений необходимо вычислить координаты и значения синусов и косинусов углов наклона касательных.
Ординаты точек оси арки и углы наклона касательных определяются по следующим уравнения:
а) при очертании оси по параболе
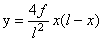 ;
; 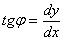 ;
;
б) при очертании оси по окружности
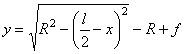 ,
,
где 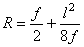 ;
; 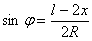 ;
; 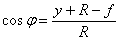 .
.
Для трехшарнирных рам ординаты и необходимые углы наклона определяются непосредственно из чертежа. Следует помнить, что для правой половины арки или рамы угол наклона касательной отрицателен.
Вычисление значений опорных реакций, моментов, поперечных и продольных сил в заданных сечениях надо иллюстрировать необходимыми формулами. На линиях влияния  ,
,  и
и 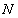 должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете. Линии влияния надо строить под схемой арки (рамы) в своем линейном масштабе.
должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете. Линии влияния надо строить под схемой арки (рамы) в своем линейном масштабе.
Расчет ПЛОСКИХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ШАРНИРНЫХ РАМ
Задача 5.1.
Для одной из рам, изображенных на рис. 5.1.1 – 5.1.26, требуется:
1) выполнить кинематический анализ;
2) определить реакции в связях, включая силы взаимодействия в шарнирах;
3) построить эпюры внутренних силовых факторов.
Исходные данные для расчета принять из табл.5.1
Таблица 5.1
| Номер строки | Схемы балок по рис. 5.1.1–5.1.26 | h, м | l, м | M, кНм | F, кН |
| 01 | 5.1.1 | 3 | 2 | 6 | 4 |
| 02 | 5.1.2 | 4 | 3 | 5 | 5 |
| 03 | 5.1.3 | 2 | 4 | 4 | 3 |
| 04 | 5.1.4 | 4 | 2 | 6 | 6 |
| 05 | 5.1.5 | 3 | 2 | 8 | 7 |
| 06 | 5.1.6 | 2 | 4 | 10 | 2 |
| 07 | 5.1.7 | 3 | 3 | 7 | 8 |
| 08 | 5.1.8 | 2 | 5 | 10 | 3 |
| 09 | 5.1.9 | 5 | 1 | 9 | 4 |
| 10 | 5.1.10 | 4 | 2 | 8 | 7 |
| 11 | 5.1.11 | 1 | 4 | 7 | 8 |
| 12 | 5.1.12 | 3 | 3 | 6 | 3 |
| 13 | 5.1.13 | 5 | 2 | 5 | 6 |
| 14 | 5.1.14 | 2 | 5 | 2 | 5 |
| 15 | 5.1.15 | 4 | 3 | 5 | 2 |
| 16 | 5.1.16 | 1 | 4 | 6 | 8 |
| 17 | 5.1.17 | 3 | 3 | 7 | 5 |
| 18 | 5.1.18 | 5 | 1 | 8 | 3 |
| 19 | 5.1.19 | 1 | 2 | 9 | 4 |
| 20 | 5.1.20 | 2 | 5 | 10 | 8 |
| 21 | 5.1.21 | 4 | 3 | 4 | 9 |
| 22 | 5.1.22 | 3 | 2 | 5 | 2 |
| 23 | 5.1.23 | 2 | 4 | 8 | 3 |
| 24 | 5.1.24 | 1 | 2 | 7 | 5 |
| 25 | 5.1.25 | 5 | 1 | 6 | 7 |
| 26 | 5.1.26 | 2 | 5 | 4 | 6 |
| 27 | 5.1.1 | 5 | 2 | 5 | 6 |
| 28 | 5.1.2 | 2 | 5 | 2 | 5 |
| 29 | 5.1.3 | 4 | 3 | 5 | 2 |
| 30 | 5.1.4 | 1 | 4 | 6 | 8 |
| 31 | 5.1.5 | 3 | 3 | 7 | 5 |
| 32 | 5.1.6 | 5 | 1 | 8 | 3 |
| 33 | 5.1.7 | 1 | 2 | 9 | 4 |
| 34 | 5.1.8 | 2 | 5 | 10 | 8 |
| 35 | 5.1.9 | 4 | 3 | 4 | 9 |
| 36 | 5.1.10 | 3 | 3 | 9 | 8 |
| г | в | б | а | в |
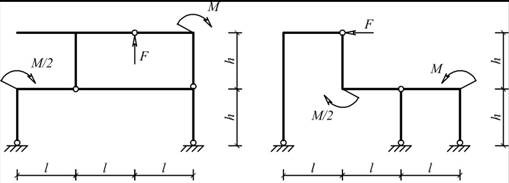
Рис.5.1.1 Рис. 5.1.2
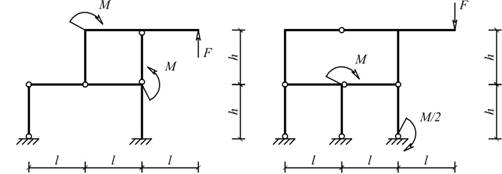
Рис. 5.1.3 Рис. 5.1.4
Рис. 5.1.5 Рис. 5.1.6
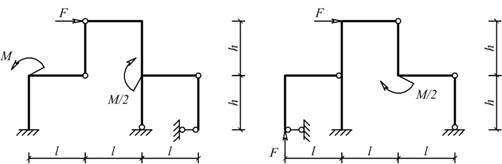
Рис. 5.1.7 Рис. 5.1.8

Рис. 5.1.9 Рис. 5.1.10
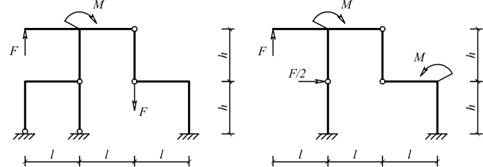
Рис. 5.1.11 Рис. 5.1.12
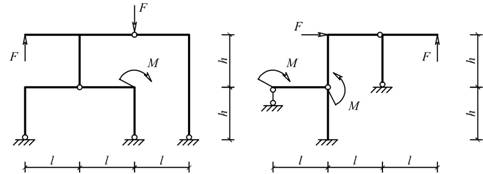
Рис. 5.1.13 Рис. 5.1.14
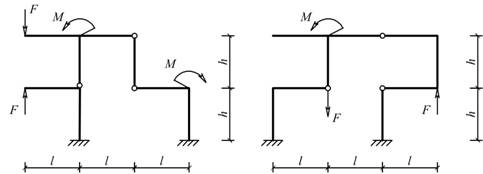
Рис. 5.1.15 Рис. 5.1.16
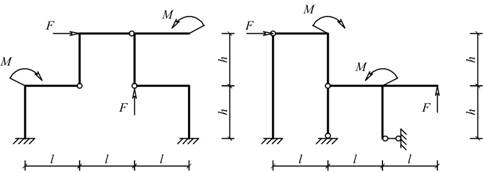
Рис. 5.1.17 Рис. 5.1.18
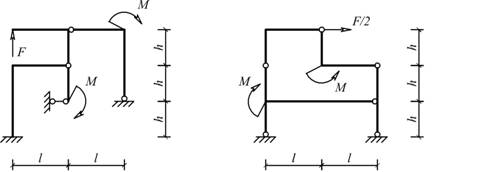
Рис. 5.1.19 Рис. 5.1.20
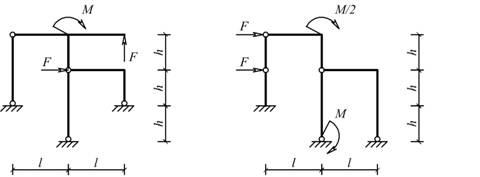
Рис. 5.1.21 Рис. 5.1.22
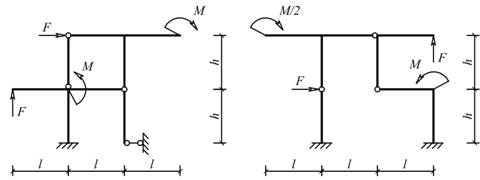
Рис. 5.1.23 Рис. 5.1.24
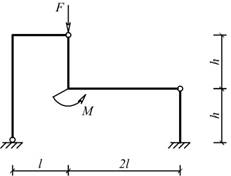

Рис. 5.1.25 Рис. 5.1.26
Пример решения задачи
Исходные данные: схема рамы на рис. 5.1.25; l= 2 м; h= 2 м; M= 4 кНм; F= 4 кН.
а) Кинематический анализ рамы
1) Степень свободы системы 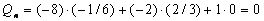
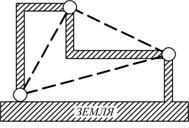
Рис. 5.1.27
2) Рама представляет собой неизменяемую фигуру (рис.5.1.27), состоящую из трех дисков, соединенных между собой шарнирами А, 1 и 2, не лежащими на одной прямой. Следовательно, геометрическая неизменяемость рамной конструкции обеспечена.
б) Реакции в связях
Силы, обеспечивающие равновесие дисков рамы, показаны на рис. 5.1.28.
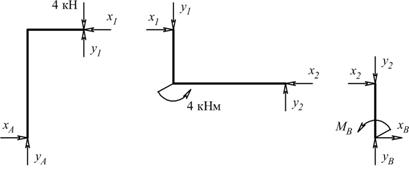
Рис. 5.1.28
Направление и величины реакций хА, уА, хВ, уВ, МВ, х1, у1, х2, у2, найденных из 9-и уравнений равновесия (по три для каждого диска), показаны на рис.5.1.29.

Рис. 5.1.29
в) Эпюры внутренних силовых факторов в дисках рамы
Эпюры продольных сил (кН)
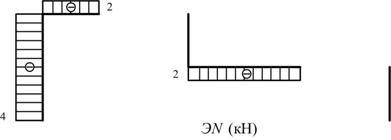
Рис. 5.1.30
Эпюры поперечных сил (кН)
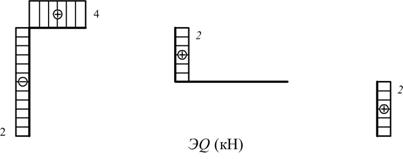
Рис. 5.1.31
Эпюры изгибающих моментов (кНм)
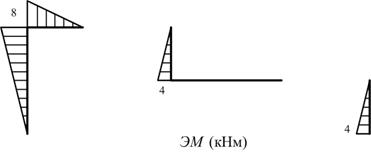
Рис. 5.1.32
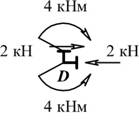
г) Проверка равновесия жестких узлов С и D
| Узел С | Узел D |
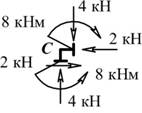
| 
|
| SX = 0; SY = 0; SMC = 0. | SX = 0; SY = 0; SMD = 0. |
 2018-02-14
2018-02-14 558
558








