 (2)
(2)
полностью характеризуется модулем Am и аргументом a, аналогичными амплитуде и фазе гармонического колебания. Комплексное число  называют комплексной амплитудой гармонического колебания (1).
называют комплексной амплитудой гармонического колебания (1).
Расчет электрических цепей при воздействии гармонического колебания становится более удобным, если воздействие задается комплексной амплитудой. Результаты расчета получаются также в виде комплексных амплитуд. По комплексным амплитудам легко определяют амплитуды и начальные фазы и записывают соответствующие гармонические функции. Метод расчета цепей, базирующийся на понятии комплексной амплитуды, называют методом комплексных амплитуд.
Метод комплексных амплитуд в электротехнике впервые в 1883 году применил немецкий ученый Ч. Штейнмец. В России метод широко использовал академик В. Ф. Миткевич.
Переход от временной функции к комплексной амплитуде обратим:
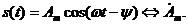 (3)
(3)
Аналогично сумма гармонических функций равных частот заменяется суммой комплексных амплитуд:
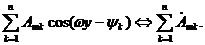
Найдем комплексные амплитуды производной и интеграла гармонического колебания. Продифференцировав равенство (1)

в соответствии с (3) получим
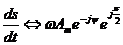 .
.
Так как  то
то
 (4)
(4)
Следовательно, дифференцирование гармонической функции соответствует умножению комплексной амплитуды на величину jw. На векторной диаграмме вектор, соответствующий производной, повернут на угол p/2 против часовой стрелки, а его модуль умножен на w. Аналогично доказывается, что:
 .(5)
.(5)
Интегрирование гармонической функции

эквивалентно делению временной функции на w и повороту фазы на -p/2:

Так как  то
то
 (6)
(6)
Таким образом, интегрирование гармонической функции соответствует делению комплексной амплитуды на величину jw. На векторной диаграмме вектор, соответствующий интегралу, повернут на угол p/2 по часовой стрелке и его модуль поделен на w.
17.1.2. СПЕКТРЫ ПЕРИОДИЧЕСКИХ КОЛЕБАНИЙ
Из курса математики известно, что любое периодическое колебание, удовлетворяющее условиям Дирихле, можно представить рядом Фурье
 (7)
(7)
где  - угловая частота периодического колебания;
- угловая частота периодического колебания;
 (8)
(8)
выражения (8) интегрируют в произвольно расположенном интервале времени, равном периоду Т. Обычно интегрирование производят от 0 до Т или от –T/2 до Т/2.
Ряд Фурье (7) показывает, что периодическое колебание можно разложить на постоянную составляющую а0/2 и совокупность гармонических колебаний с кратными частотами:
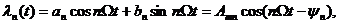 (9)
(9)
где
 (10)
(10)
Обратное представление (10):
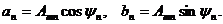 (11)
(11)
Гармонические колебания (9) называют гармониками, величину Amn – амплитудой, yn – начальной фазой n -ой гармоники. Разложение периодического колебания на гармоники позволяет ввести очень важное для радиотехники понятие спектра колебания. Амплитудным спектром периодического колебания называют функцию, отражающую зависимость амплитуд гармоник от частоты. При графическом изображении амплитудного спектра по оси абсцисс откладывают частоту, а по оси ординат – амплитуду гармоник (рис. 17.3, а).
 Фазовым спектром называют функцию, отражающую зависимость фаз гармоник от частоты (рис. 17.3, б).
Фазовым спектром называют функцию, отражающую зависимость фаз гармоник от частоты (рис. 17.3, б).
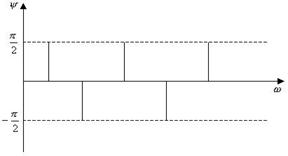
а) б)
Рис. 17.3
Ширину спектра DF определяют как разность наибольшей и наименьшей частот полосы, в пределах которой амплитуды гармоник превышают некоторым образом определенную минимальную амплитуду:
 (12)
(12)
В таблице 1 приведены примеры наиболее часто встречающихся периодических колебаний, ряды Фурье и графики амплитудных спектров. Для каждого примера указана ширина спектра, определенная на уровне 0,1 амплитуды первой гармоники.
Из таблицы видно, что наибольшей шириной спектра обладают последовательности прямоугольных и пилообразных импульсов. Ширина спектра колебаний уменьшается по мере уменьшения максимальной скорости изменения временной функции колебания. Следует обратить внимание на то, что спектр гармонического колебания одна линия.
В задачах анализа цепей при воздействии периодических колебаний удобно пользоваться комплексным рядом Фурье. Такой ряд получается, если временную функцию n-ой гармоники записать, используя формулу Эйлера, в виде суммы показательных функций:
 (13)
(13)
Введя комплексные амплитуды
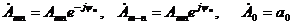
и подставив (13) в (7), получим
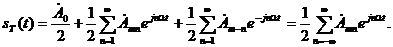 (14)
(14)
Этот ряд называют комплексным рядом Фурье.
 2018-02-20
2018-02-20 288
288








