 (19)
(19)
Модуль этой функции S(w) называют амплитудной спектральной плотностью или просто амплитудным спектром колебания, а его фазу y(w) – фазовым спектром. Амплитудный спектр – функция четная, а фазовый – нечетная, поэтому графики этих функций достаточно изображать только на положительной полуосью частот. Примеры спектральных плотностей непериодических колебаний приведены в таблице 2.
Преобразование Фурье с математической точки зрения обладает существенным недостатком – вычисление функции спектральной плотности возможно только для колебаний с конечной энергией, для которых
 (20)
(20)
где С – конечная величина.
Более универсальным является преобразование Лапласа
 (21)
(21)
формально получаемое из преобразования Фурье отбрасываем отрицательной части временной оси и заменой мнимого аргумента jw на комплексный  Иначе говоря, преобразование Лапласа предполагает введение вспомогательного множителя
Иначе говоря, преобразование Лапласа предполагает введение вспомогательного множителя  благодаря чему интеграл (21) становится конечным и для колебаний, не удовлетворяющих равенству (20).
благодаря чему интеграл (21) становится конечным и для колебаний, не удовлетворяющих равенству (20).
Преобразование Лапласа, как и преобразование Фурье, обратимо. Обратное преобразование Лапласа
 (22)
(22)
Интегрирование производится на комплексной плоскости параллельно мнимой оси.
Результат преобразования Лапласа – функцию  - часто называют изображением функции S(t) [тогда S(t) называют оригиналом]. Математически функция
- часто называют изображением функции S(t) [тогда S(t) называют оригиналом]. Математически функция  эквивалентна функции спектральной плотности
эквивалентна функции спектральной плотности  , поэтому ее иногда называют спектральной плотностью комплексной переменной. Из-за меньшей физической наглядности преобразование Лапласа в инженерной практике используют только как математическое средство, удобное при решении задач прохождения колебаний произвольной формы через линейные цепи.
, поэтому ее иногда называют спектральной плотностью комплексной переменной. Из-за меньшей физической наглядности преобразование Лапласа в инженерной практике используют только как математическое средство, удобное при решении задач прохождения колебаний произвольной формы через линейные цепи.
17.2. СВОЙСТВА ПРЕОБРАЗОВАНИЙ ФУРЬЕ И ЛАПЛАСА
Изучение спектров колебаний значительно упрощается, если воспользоваться некоторыми свойствами интегральных преобразований Фурье и Лапласа. Иногда эти свойства называют теоремами о спектрах.
1. Связь между спектрами одиночного импульса и периодической последовательностью таких же импульсов. Рассматривается одиночный импульс s(t) длительности  . Такой импульс
. Такой импульс  только в интервале от 0 до
только в интервале от 0 до  , поэтому спектральную плотность можно определить, используя (17), но интегрируя не в бесконечных пределах, а от 0 до некоторого значения
, поэтому спектральную плотность можно определить, используя (17), но интегрируя не в бесконечных пределах, а от 0 до некоторого значения 
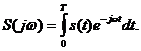 (23)
(23)
Импульс s (t) можно сдвинуть во времени на ±пТ (п= 1, 2,...) и все импульсы сложить, тогда получим периодическое колебание: sT (t) =...+ s (* + 2T) + s(t + Т) + S(t) + s(t — T) + s(t — 2T)+....
Коэффициенты ряда Фурье данного периодического колебания определяются формулой (15):
 (15а)
(15а)
где W=2p/ T.
Сравнивая (23) и (15а) и учитывая, что в рассматриваемом интервале от 0 до Т функции s(t) и sT(t) равны, находим  отсюда следует, что коэффициенты ряда Фурье пропорциональны функции спектральной плотности S (jw) в точках w=nW..
отсюда следует, что коэффициенты ряда Фурье пропорциональны функции спектральной плотности S (jw) в точках w=nW..
На рис. 17.4 изображены сигналы и соответствующие им спектры: одиночный прямоугольный импульс, периодическая последовательность прямоугольных импульсов с периодом T 1, а также последовательность с периодом T2 > T1. Из рисунка видно, что формаогибающей составляющих спектра

Рис. 17.4
периодической последовательности определяется формой импульса, а частота — периодом импульсов. В дальнейшем не будем разделять понятия спектра периодического колебания и функции спектральной плотности непериодического колебания и назовем их одинаково - спектром.
Следующие свойства приводятся без доказательств. При этом используется обозначение F[s(t)]=S(jw).
2. Преобразование Фурье является линейным, т. е. спектр суммы колебаний равен сумме спектров этих колебаний:
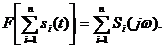 (24)
(24)
3. Увеличение амплитуды колебания s (t) в а раз приводит к увеличению в а раз амплитуд составляющих спектра:
 (25)
(25)
4. Увеличение масштаба времени колебания в а раз приводит к уменьшению в а раз амплитуд составляющих спектра и ширины частотной полосы спектра:
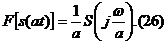
Это очень важное свойство для передачи сигналов по каналам связи, так как показывает, что, например, широкополосные сигналы можно передавать по узкополосным каналам, растянув сигналы во времени (путем записи, к примеру, на магнитную ленту и воспроизведения с пониженной скоростью движения ленты).
5. Задержка колебания на t эквивалентна умножению его спектра на множитель e-jwt:
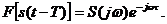 (27)
(27)
6. Дифференцирование колебания эквивалентно умножению его спектра на jw:
 (28)
(28)
7. Интегрирование колебания эквивалентно делению его спектра на jw:
 (29)
(29)
Свойства, аналогичные 2-7, справедливы и для преобразования Лапласа:
2a. 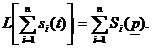
3a. 
4a. 
5a. 
6a. 
7a. 
17.3. МОЩНОСТЬ КОЛЕБАНИЙ
Когда к цепи подключен источник переменной ЭДС, токи и напряжения в ветвях цепи являются переменными, поэтому мгновенная мощность на некотором элементе цепи, равная произведению мгновенных значений тока и напряжения p(t) = i(t) и (t), также является переменной.
Так как мгновенные значения тока и напряжения могут быть как положительными, так и отрицательными, то и мгновенная мощность также может быть положительной и отрицательной величиной. Когда мгновенная мощность положительная, то цепь получает энергию от источника, а когда отрицательная, то цепь возвращает источнику накопленную энергию.
Энергия, переданная источником элементу цепи за промежуток времени 
 (30)
(30)
Средняя мощность
 (31)
(31)
Средняя мощность периодического колебания постоянна за период, поэтому ее можно вычислить интегрированием (30) в пределах О, Т, где T = t2 — t1.
Для удобства расчета мощности в цепях переменного тока вводят понятия действующих значений напряжения и тока

 (32)
(32)
численно равных постоянным напряжению и току, при которых выделяется мощность, равная средней за период мощности переменного колебания.
Действующие значения гармонических напряжений и тока пропорциональны амплитудам:


17. 3.1. МОЩНОСТЬ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Пусть в некоторой ветви цепи течет ток и падает напряжение, соответственно  и
и  тогда средняя за период мощность равна
тогда средняя за период мощность равна
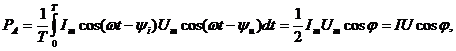 (33)
(33)
где 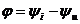 — активная мощность. Она максимальна тогда, когда фазы тока и напряжения совпадают (
— активная мощность. Она максимальна тогда, когда фазы тока и напряжения совпадают ( ). При этом цепь потребляет максимальную энергию.
). При этом цепь потребляет максимальную энергию.
Наряду со средней активной мощностью вводится полная мощность, равная произведению действующих значений напряжения и тока:
 (34)
(34)
и реактивная мощность, равная произведению действующих значений напряжения и тока, умноженных на sinj:
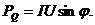 (35)
(35)
Реактивная мощность характеризует процессы обмена энергией между цепью и источником и численно равна максимальной скорости запаса энергии в цепи.
Полная мощность
 (36)
(36)
Коэффициент cosj в формуле активной мощности называют коэффициентом мощности; он показывает, какую долю полной мощности составляет активная мощность. Коэффициент мощности является важным показателем устройств энергетического обеспечения.
Когда расчет цепи производят методом комплексных амплитуд и найдены, например, комплексные амплитуды 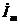 и
и 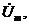 то полную комплексную мощность вычисляют по формуле
то полную комплексную мощность вычисляют по формуле
 (37)
(37)
либо 
где  - сопряженная комплексная амплитуда тока (если
- сопряженная комплексная амплитуда тока (если  то
то  ). Активная и реактивная мощности соответственно
). Активная и реактивная мощности соответственно
 (38)
(38)
 (39)
(39)
17.3.2. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО КОЛЕБАНИЯ
Средняя мощность периодического колебания, выделяющаяся на единичном сопротивлении R = 1 Ом, в общем случае равна
 (40)
(40)
Подставим в (40) ряд Фурье:

Возведя этот ряд в квадрат и проинтегрировав его почленно, с учетом того, что



получим
 (41)
(41)
Таким образом, средняя мощность периодического колебания равна сумме мощностей всех гармоник и постоянной составляющей. Мощность каждой гармоники пропорциональна квадрату амплитуды этой гармоники; следовательно, средняя мощность в спектре распределена пропорционально квадратам амплитуд гармоник.
Если в (41) бесконечную сумму заменить суммой N ее первых членов:
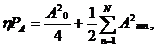 (42)
(42)
то получим мощность  (h< 1) в полосе частот, соответствующей ширине спектра
(h< 1) в полосе частот, соответствующей ширине спектра  . Равенство (12) может служить критерием определения ширины спектра колебания. Например, выбрав h=0,95, можно найти такое значение Nh, для которого правая часть выражения (42) будет иметь значение, не меньшее 0,95РA; тогда ширина спектра равна NhF.
. Равенство (12) может служить критерием определения ширины спектра колебания. Например, выбрав h=0,95, можно найти такое значение Nh, для которого правая часть выражения (42) будет иметь значение, не меньшее 0,95РA; тогда ширина спектра равна NhF.
17.3.3. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО КОЛЕБАНИЯ
Энергия колебания s (t), выделяющаяся на единичном сопротивлении,
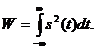 (43)
(43)
Это равенство можно записать в виде

Изменяя порядок интегрирования, имеем
 . (44)
. (44)
Интеграл
 (45)
(45)
Подставив (45) в (44), получим следующее выражение для энергии сигнала:

Так как функция S2 (w) является четной, то
 (46)
(46)
Выражение (46) называют равенством Парсеваля.
Величина 2S2(2pf)df показывает, какая часть энергии сигнала приходится на полосу частот шириной df. Если df = l,то величина 2S2(2pf) показывает, какая часть энергии сигнала приходится на полосу частот шириной 1Гц при заданной частоте f. Таким образом, квадрат модуля спектра колебания показывает, как энергия колебания распределяется на оси частот, и называется спектральной плотностью энергии сигнала.
Равенство Парсеваля позволяет определить ширину спектра DF как полосу частот, в которую попадает основная доля (h < 1) энергии колебания:
 (47)
(47)
В Рассмотренные спектральные представления непериодических колебаний справедливы только для колебаний с конечной энергией, так как только при этом условии интегралы (17), (43) и (46) ограничены. Этому требованию удовлетворяют все колебания ограниченной амплитуды и конечной длительности, а также колебания неограниченной длительности, мгновенные значения которых ограничены и при  уменьшаются не медленнее чем
уменьшаются не медленнее чем 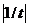 .
.
17.4. СЛУЧАЙНЫЕ КОЛЕБАНИЯ
Математической моделью случайных сигналов и помех является
случайный процесс X(t). В фиксированный момент времени t = t1 отсчет процесса X(t1) = x1 — случайная величина, описываемая плотностью распределения вероятностей * W (x1,t1). Для описания случайного процесса в п фиксированных моментов времени t1...., tn используется n-мерная плотность распределения вероятностей 
Каждое наблюдение случайного процесса (например, на экране осциллографа) — различная функция xi(t), i =l, 2,... (рис. 5). Функции Xi(t) называют выборочными или реализациями случайного процесса. Достаточно большой набор реализаций дает определенное представление о случайном процессе. По нему находятся вероятностные характеристики процесса.

Рис. 17.5
Многомерные плотности распределения вероятности при больших п достаточно точно описывают случайный процесс. Однако ввиду сложности такое описание используется только в теоретических исследованиях. Экспериментально с разумными затратами можно измерить одномерную (n=1) или двумерную (п=2) плотности распределения вероятностей.
Среди множества различных процессов особое место занимает гауссовский случайный процесс. Его одномерная плотность распределения вероятностей
 (48)
(48)
где m(t) и s(t) —математическое ожидание и среднеквадратическое отклонение.
Исключительное значение гауссовского случайного процесса в прикладных задачах объясняется тем, что, как следует из центральной предельной теоремы Ляпунова, плотность распределения вероятности суммы независимых или слабозависимых равномерно малых слагаемых при неограниченном увеличении их числа приближается к плотности распределения вероятности гауссовского случайного процесса. Поэтому шумы и помехи, а также сигналы, которые порождаются большим числом независимых источников, имеют плотность распределения вероятностей, близкую к гауссовской.
Кроме плотностей распределения вероятностей для описания свойств случайных процессов используются также моментные функции. Из них наиболее часто используются: математическое ожидание
 (49)
(49)
 (50)
(50)

 (51)
(51)
По определению, математическое ожидание представляет среднее значение случайного процесса. Когда рассматриваемый случайный процесс состоит из детерминированного сигнала s(t) и случайного шума n(t) снулевым средним значением, т. е. x(t)=s(t)+ n(t), то математическое ожидание процесса x(t) равно сигналу s(t). В частном случае, когда s(t) -постоянная составляющая процесса x(t), то и математическое ожидание - постоянная величина.
Дисперсия характеризует рассеяние случайного процесса. По определению, дисперсия — среднее значение квадрата величины, и, таким образом, она пропорциональна средней мощности центрированного процесса 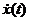 = x(t)-m(t). Как видно из (50), среднеквадратическое отклонение
= x(t)-m(t). Как видно из (50), среднеквадратическое отклонение  имеет ту же размерность, что и сам процесс. Физический смысл величины s(t) - действующее значение напряжения или тока центрированного случайного процесса.
имеет ту же размерность, что и сам процесс. Физический смысл величины s(t) - действующее значение напряжения или тока центрированного случайного процесса.
Корреляционная функция - мера связи между отсчетами случайного процесса, взятыми в моменты времени t1 и tz. Когда t1 = t2, то, очевидно, В (t1, t2) = D(t1), поэтому максимальное значение корреляционной функции равно дисперсии. Если моменты времени t1 и t2 так удалены друг от друга, что никакой связи между значениями процесса нет, то двумерная плотность распределения вероятностей выражается произведением одномерных плотностей

При этом условии корреляционная функция (51) становится равной нулю.
В качестве математической модели помехи часто используется стационарный случайный процесс, свойства которого не зависят от положения начального отсчета. Математическое ожидание и дисперсия стационарного случайного процесса не зависят от времени: m(t)=m,  а корреляционная функция зависит только от расстояния между отсчетами
а корреляционная функция зависит только от расстояния между отсчетами  .
.
Многие случайные процессы, такие, как шумы электронных приборов и каналов связи, обладают свойством эргодичности, заключающейся в том, что средние значения функций случайного процесса, найденные путем усреднения по реализациям, совпадают с соответствующими средними, найденными путем усреднения одной реализации во времени.
Для эргодических случайных процессов математическое ожидание, дисперсия и корреляционная функция, представленные выражениями (49), (50) и (51), совпадают соответственно со следующими выражениями:


 (52)
(52)
Свойство эргодичности особенно ценно при экспериментальных исследованиях случайных процессов. Для нахождения средних характеристик таких процессов не нужно располагать большим числом источников, создающих отдельные реализации процесса, а достаточно одной реализации и, следовательно, одного источника.
Спектральные представления, базирующиеся на преобразовании Фурье, применимы только к отдельным реализациям случайного процесса. Средняя спектральная плотность, найденная путем усреднения совокупности спектральных плотностей отдельных реализаций процесса, из-за случайности их фазовых характеристик равна нулю. Поэтому для представления спектральных характеристик случайного процесса вводят понятие спектральной плотности мощности, характеризующее распределение мощности процесса на частотной оси.
Спектральная плотность мощности эргодического процесса находится по одной реализации и определяется выражением
 (53)
(53)
где 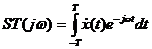 - спектральная плотность реализации центрированного процесса
- спектральная плотность реализации центрированного процесса  (t) = x(t) - m.
(t) = x(t) - m.
Спектральная плотность мощности неэргодического процесса находится путем усреднения по реализациям спектральных плотностей мощности отдельных реализаций, определенных выражением (53). Нужно обратить внимание, что спектральная плотность мощности G(w), как и спектральная плотность S (jw), определена как при положительных, так и при отрицательных частотах. Физическое содержание этого понятия противоречит его определению на отрицательной полуоси. Поэтому в инженерной практике чаще всего используют спектральную плотность мощности, определенную только на положительной полуоси частот, т. е.
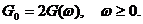 (54)
(54)
Средняя мощность процесса через спектральную плотность мощности
выражается интегралом, аналогичным (46):
 (55)
(55)
В заданной полосе частот f1 - f2 мощность случайного процесса
 (56)
(56)
Спектральная плотность мощности стационарного случайного процесса однозначно связана с корреляционной функцией преобразованием Фурье (теорема Хинчина - Винера):
 (57)
(57)
Так как преобразование Фурье обратимо, то корреляционная функция через спектральную плотность мощности выражается обратным преобразованием Фурье:
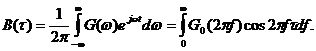 (58)
(58)
Указанная связь между спектральной плотностью мощности и корреляционной функцией аналогична связи между спектральной плотностью и временной функцией детерминированного сигнала. В частности, в свойства преобразования Фурье применимы и к спектральной плотности мощности, и к корреляционной функции.
В качестве модели помехи часто используется «белый шум», характерная особенность которого заключается в том, что его спектральная плотность мощности постоянна во всем диапазоне частот (от 0 до  ). Такая модель описывает идеальный шум. Как следует из (54), средняя мощность такого шума должна быть бесконечной.
). Такая модель описывает идеальный шум. Как следует из (54), средняя мощность такого шума должна быть бесконечной.
Для некоторого устройства помеха считается «белым шумом», если ее спектральная плотность мощности постоянна в полосе частот более широкой, чем полоса пропускания устройства. В полосе частот f1-f2 в соответствии с (56) мощность «белого шума»
 (59)
(59)
Эта мощность пропорциональна ширине полосы частот f2 - f1.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Чем отличается сигнал от помехи?
2. Чем отличается аналоговый сигнал от цифрового?
3. Сигнал телевизионной станции - детерминированный или случайный?
4. Можно ли использовать случайный сигнал в качестве измерительного
сигнала?
5. В чем достоинства гармонических колебаний, обусловливающие их широкое применение?
6. Укажите, что общего между электрическим гармоническим колебанием и вектором на плоскости и чем они отличаются.
7. Как известно, негармоническое периодическое колебание можно представить в виде суммы гармонических колебаний. А можно ли генерировать негармонические колебания с помощью генераторов гармонических колебаний? Если можно, то как? Составьте функциональную схему.
8. Почему для получения спектрального представления непериодических сигналов используется преобразование Фурье, а не разложение в ряд Фурье?
9. В чем преимущества преобразования Фурье перед преобразованием Лапласа, и наоборот?
10. Можно ли телевизионный сигнал, занимающий полосу частот 0 - 6,5 МГц, передать по телефонному каналу с полосой пропускания 3,4 кГц? Если можно, то как?
11. Почему отдельно определяются и измеряются активная и реактивная мощности?
12. Можно ли узнать содержание произнесенной в микрофон фразы по корреляционной функции, измеренной с помощью коррелометра, на вход которого подан сигнал с микрофона?
13. Какой шум для человеческого слуха можно считать белым: шелест леса, шум моря, шум улицы?
Таблица 2.1
| Колебание | Ряд Фурье | Амплитудный спектр | |
 |  sT 1 -T –T/2 0 T/2 T t sT 1 -T –T/2 0 T/2 T t |  |  Am 0,5 Am 0,5  0,4 0,3 0,2 0,1 0 W 3W 5W f 0,4 0,3 0,2 0,1 0 W 3W 5W f |
 |  sT f -T 0 T 2T t sT f -T 0 T 2T t |  |  Am 0,5 0,4 Am 0,5 0,4  0,3 0,2 0,1 0 2W 4W 6W 8W 10W 12W w 0,3 0,2 0,1 0 2W 4W 6W 8W 10W 12W w |
Продолжение таблицы 2.1
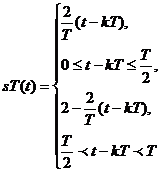 |  sT 1 T T/2 0 T/2 T t sT 1 T T/2 0 T/2 T t |  |  Am 0,5 Am 0,5  0,4 0,3 0,2 0,1 0 W 3W 5W 7W 9W 11W 13W w 0,4 0,3 0,2 0,1 0 W 3W 5W 7W 9W 11W 13W w | |||
 | sT
1
-T/2 0 T/2 T t | 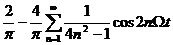 |  Am 0,6 0,5 Am 0,6 0,5  0,4 0,3 0,2 0,1 0 2W 4W 6W w 0,4 0,3 0,2 0,1 0 2W 4W 6W w |
Таблица 2.2
| Сигнал | Спектральная плотность | ||
 | 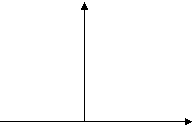 S 0 t S 0 t |  |  S 1 0 w S 1 0 w |
 | 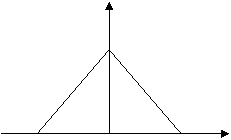 S 1 S 1 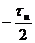 0 0   t t |  |  S S  0 0   w w |
Продолжение таблицы 2.2
 |  |  | S   0 0   w w |
  |  S 1 S 1  0 0  t t |  |  S S  0 0  w w |
 2018-02-20
2018-02-20 2773
2773
