Рассмотрим ряд 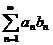 , где
, где 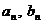 - две последовательности вещественных чисел.
- две последовательности вещественных чисел.
Признак Абеля: Если ряд 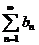 сходится, а числа
сходится, а числа 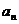 образуют монотонную и ограниченную последовательность, то ряд
образуют монотонную и ограниченную последовательность, то ряд 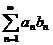 сходится.
сходится.
Признак Дирихле: Если частичные суммы ряда 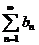 в совокупности ограничены, а числа
в совокупности ограничены, а числа 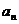 образуют монотонную последовательность, стремящуюся к нулю, то ряд
образуют монотонную последовательность, стремящуюся к нулю, то ряд 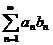 сходится.
сходится.
Примеры решения задач:
Исследовать на сходимость ряды:
1. 
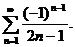
Ряд, составленный из абсолютных членов, расходится по предельному признаку сравнения с рядом  . Оба условия Лейбница выполняются:
. Оба условия Лейбница выполняются: 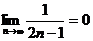 и
и 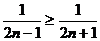 .
.
Значит, исходный ряд сходится условно.
2.  .
.
Рассмотрим ряд из модулей 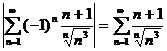 . Сравним его с рядом
. Сравним его с рядом  , воспользовавшись предельным признаком сравнения:
, воспользовавшись предельным признаком сравнения: 
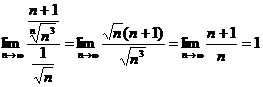 .
.
Ряд  расходится как гармонический с
расходится как гармонический с 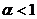 .
.
.
Ряд из модулей расходится, значит, наш знакопеременный ряд не обладает абсолютной сходимостью, но он сходится условно согласно признаку Лейбница, т.к.  для любых значений
для любых значений  и
и  .
.
Ответ: сходится условно.
3. 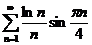 .
.
Решение:  , рассмотрим
, рассмотрим 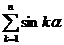 .
.
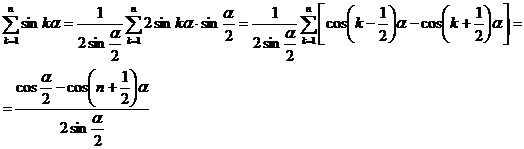
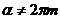
Поэтому 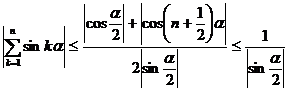 .
.
Т.е. при 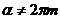 все рассматриваемые суммы ограничены. В нашем случае
все рассматриваемые суммы ограничены. В нашем случае 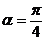 .
.
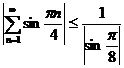 .
.
Таким образом, ряд сходится по признаку Дирихле.
Приближенное вычисление суммы ряда
Вычислить сумму знакочередующегося числового ряда 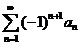 , с заданной точностью
, с заданной точностью 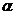 .
.
1. Если 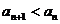 и
и 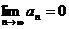 , то для остатка знакочередующегося ряда
, то для остатка знакочередующегося ряда 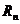 справедливо неравенство
справедливо неравенство 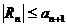 , т.е. остаток ряда меньше по модулю первого отброшенного члена ряда.
, т.е. остаток ряда меньше по модулю первого отброшенного члена ряда.
2. Если 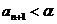 , то и
, то и 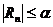 . Поэтому, решая неравенство
. Поэтому, решая неравенство 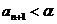 , находим количество членов ряда, которое необходимо взять для вычисления суммы ряда с заданной точностью
, находим количество членов ряда, которое необходимо взять для вычисления суммы ряда с заданной точностью 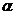 .
.
3. Непосредственно вычисляем  -ю частичную сумму ряда
-ю частичную сумму ряда
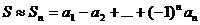 .
.
Задача 9. Вычислить сумму ряда с точностью 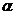 .
.
 ,
, 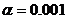 .
.
Сумма ряда 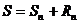 ,
,
где 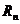 – остаток ряда. По условию задачи
– остаток ряда. По условию задачи 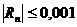 . Для знакочередующихся рядов остаток ряда меньше по модулю первого отброшенного члена ряда, поэтому
. Для знакочередующихся рядов остаток ряда меньше по модулю первого отброшенного члена ряда, поэтому
 .
.
Последнее неравенство выполняется при 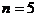 , значит достаточно оставить только первые пять членов ряда:
, значит достаточно оставить только первые пять членов ряда:
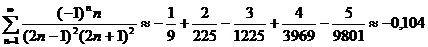
 2018-02-20
2018-02-20 2822
2822
