Доказать, исходя из определения, равномерную сходимость функционального ряда
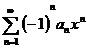 на отрезке
на отрезке  . При каких
. При каких  абсолютная величина остаточного члена ряда не превосходит
абсолютная величина остаточного члена ряда не превосходит 
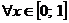 ?
?
Функциональный ряд  называется равномерно сходящимся на отрезке
называется равномерно сходящимся на отрезке  , если для любого как угодно малого
, если для любого как угодно малого  найдется такой номер
найдется такой номер  , что при всех
, что при всех 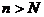 будет выполняться неравенство
будет выполняться неравенство  для любого
для любого 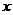 из отрезка
из отрезка  .
.
1. Т.к.  , то имеем знакочередующийся ряд. Для знакочередующегося ряда остаток
, то имеем знакочередующийся ряд. Для знакочередующегося ряда остаток  ряда меньше по модулю первого отброшенного члена ряда, поэтому
ряда меньше по модулю первого отброшенного члена ряда, поэтому
 .
.
2. На отрезке 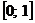 имеем
имеем  .
.
3. Решая неравенство  , находим такой номер
, находим такой номер  , что при всех
, что при всех 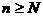 будет выполняться неравенство
будет выполняться неравенство
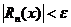
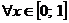 .
.
13.Доказать, исходя из определения, равномерную сходимость функционального ряда на отрезке 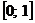 . При каких
. При каких  абсолютная величина остаточного члена ряда не превосходит 0.1
абсолютная величина остаточного члена ряда не превосходит 0.1 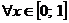 ?
?
 .
.
Решение:
Ряд называется равномерно сходящимся на отрезке  , если для всякого
, если для всякого  можно найти такой номер
можно найти такой номер  , что при
, что при 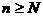 и любом
и любом  модуль остатка ряда
модуль остатка ряда 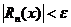 . Остаток знакочередующегося ряда меньше по модулю первого отброшенного члена ряда, поэтому на отрезке
. Остаток знакочередующегося ряда меньше по модулю первого отброшенного члена ряда, поэтому на отрезке 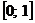

откуда  , значит,
, значит,  .
.
Т.е. для  и
и  и при любых
и при любых 

 .
.
Признак Вейерштрасса: Если  при
при  и числовой ряд
и числовой ряд  сходится, то функциональный ряд сходится на отрезке
сходится, то функциональный ряд сходится на отрезке  абсолютно и равномерно.
абсолютно и равномерно.
14. Доказать, что функциональный ряд  сходится абсолютно и равномерно для
сходится абсолютно и равномерно для  .
.
Решение: Воспользуемся тем, что 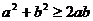 . Запишем для знаменателя
. Запишем для знаменателя  .
.
Тогда по признаку Вейерштрасса  .
.
Ряд  сходится как гармонический с
сходится как гармонический с  . Значит, исходный ряд сходится абсолютно и равномерно.
. Значит, исходный ряд сходится абсолютно и равномерно.
15. Найти сумму ряда 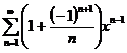 .
.
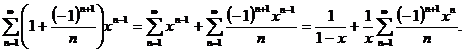
 . Найдём сумму этого ряда почленным дифференцированием:
. Найдём сумму этого ряда почленным дифференцированием:  Теперь остаётся проинтегрировать это выражение:
Теперь остаётся проинтегрировать это выражение: 
Окончательно,  .
.
Ряд Тейлора
Если функция 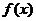 в некоторой окрестности
в некоторой окрестности 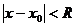 точки
точки  допускает разложение в степенной ряд
допускает разложение в степенной ряд  по степеням
по степеням  , то этот ряд называется рядом Тейлора.
, то этот ряд называется рядом Тейлора.  - значение производной к - го порядка в точке
- значение производной к - го порядка в точке  . При
. При  ряд Тейлора принято называть рядом Маклорена. Формула справедлива, если при
ряд Тейлора принято называть рядом Маклорена. Формула справедлива, если при 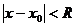 остаточный член ряда Тейлора
остаточный член ряда Тейлора  при
при  .
.
Для оценки остаточного члена можно пользоваться формулой Лагранжа:
 , где
, где 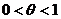 .
.
Необходимо помнить следующие пять основных разложений (в скобках указана область сходимости ряда):
-


-
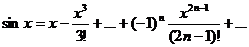

-


-


-

 .
.
16. Разложить функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням 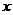 .
.
Представим функцию в виде  .
.
Воспользуемся готовым разложением 
Заменим 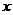 на
на  ,
,  .
.
Получим 
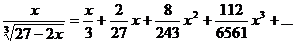
17. Разложить функцию  в ряд по степеням
в ряд по степеням 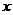 .
.
Решение:  . Находим производные данной функции:
. Находим производные данной функции:  ,
,  .
.
Далее  ,
,  и т.д. Вообще если
и т.д. Вообще если  - чётное
- чётное 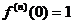 , а если
, а если  - нечётное, то
- нечётное, то
 .
.
Подставляя в формулу Тейлора, имеем: 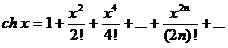 .
.
Для определения области сходимости применим признак Даламбера. Имеем:
 для любых
для любых 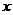 . Значит,
. Значит, 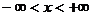 .
.
Остаточный член по формуле Лагранжа для нечётных  :
:  ; для чётных
; для чётных
 :
:  .
.
Т.к. 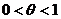 , то
, то  ,
, 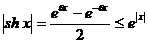 и поэтому
и поэтому
 . Ряд с общим членом
. Ряд с общим членом  сходится при любом
сходится при любом 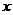 , поэтому в соответствии с необходимым признаком сходимости
, поэтому в соответствии с необходимым признаком сходимости  .
.
18. Вычислить интеграл  с точностью до 0,001.
с точностью до 0,001.
Решение: т.к.  , то данный интеграл равен
, то данный интеграл равен

 2018-02-20
2018-02-20 1519
1519