Радикальный признак Коши

Исследовать сходимость ряда с положительными членами и существует и легко вычисляется.

Радикальный признак Коши. Пусть дан ряд с положительными членами .

Если существует предел

,

то при ряд сходится, при – расходится. Если , то признак Коши ответа не дает и требуется дополнительное исследование ряда.

1. Проверяем, что 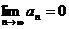, т.к. если , то ряд расходится (не выполнено необходимое условие сходимости ряда).

2. Проверяем, что для всех .

3. Вычисляем предел .

4. Применяем радикальный признак Коши и делаем вывод о сходимости или расходимости исследуемого ряда.

Замечание 1. Если общий член исследуемого ряда имеет сложный вид, то в таком случае следует воспользоваться предельным признаком сравнения и применить радикальный признак Коши к упрощенному ряду.

Замечание 2. Полезно иметь в виду, что , ,  ().

Примеры решения задач:

Исследовать на сходимость ряд .

Воспользуемся радикальным признаком Коши: .

Т.е. исследуемый ряд сходится.