Найти область сходимости функционального ряда 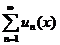 .
.
При каждом допустимом значении 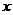 рассматриваем данный ряд как числовой и исследуем его сходимость, применяя теоремы сравнения, признаки Коши, Даламбера и др. Совокупность таких значений
рассматриваем данный ряд как числовой и исследуем его сходимость, применяя теоремы сравнения, признаки Коши, Даламбера и др. Совокупность таких значений 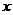 образует область сходимости ряда.
образует область сходимости ряда.
Алгоритм исследования:
1. Находим 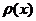 по одной из формул (если предел существует)
по одной из формул (если предел существует) 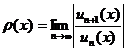 или
или 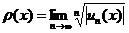 .
.
2. Находим область сходимости, решая неравенство 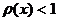 .
.
3. Исследуем поведение ряда в граничных точках области сходимости.
Найти область сходимости функционального ряда.
Пример 1. 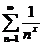 .
.
Решение: Воспользуемся признаком Даламбера 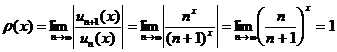 .
.
Значит, признак Даламбера не работает. Воспользуемся сходством с гармоническим рядом. Имеем сходимость при 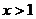 , расходимость при
, расходимость при 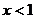 .
.
Пример 2. 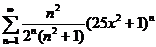 .
.
Воспользуемся радикальным признаком Коши:
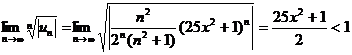 ,
,
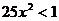 , значит,
, значит, 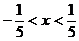 .
.
Исследуем сходимость на концах интервала: 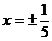
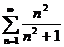 - расходится, так как не выполняется необходимый признак сходимости ряда.
- расходится, так как не выполняется необходимый признак сходимости ряда.
Область сходимости: 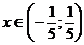 .
.
Область сходимости степенного ряда
Найти область сходимости степенного ряда 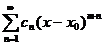 ,
,
Где 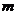 – целое число не равное нулю.
– целое число не равное нулю.
1. Находим 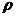 по одной из формул:
по одной из формул: 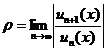 или
или 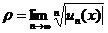 .
.
где 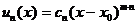 – общий член ряда. По признакам Даламбера или Коши ряд сходится при
– общий член ряда. По признакам Даламбера или Коши ряд сходится при 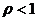 и расходится при
и расходится при 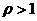 . Для определения области сходимости, решаем неравенство
. Для определения области сходимости, решаем неравенство 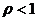 .
.
2. Исследуем поведение степенного ряда в граничных точках.
Можно найти радиус сходимости степенного ряда по формуле 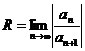 , а затем область сходимости из условия
, а затем область сходимости из условия 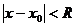 .
.
 2018-02-20
2018-02-20 356
356








