Найти область сходимости степенного ряда

Пример 1.

.

Воспользуемся радикальным признаком Коши:

.

Решая последнее неравенство, получим 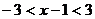, или .

Исследуем сходимость на концах интервала: .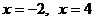

При подстановке в исходный ряд имеем 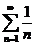– ряд расходится (гармонический ряд).

Ответ: область сходимости: .

Пример 2.

.

Воспользуемся признаком Даламбера:

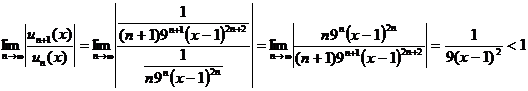
Решая последнее неравенство, получим , или

Исследуем поведение ряда на границах: при подстановке в исходный ряд  получим расходящийся гармонический ряд .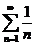

Область сходимости: .

Пример 3.  Найти область сходимости степенного ряда

 - радиус сходимости.

Область сходимости

Исследуем сходимость на концах интервала

* расходится, т.к.

* расходится, т.к.

Область сходимости .