Формула (9.5) умножения вероятностей обобщается на случай произвольного конечного числа событий. Вероятность того, что произойдет каждое из событий 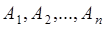 равна
равна
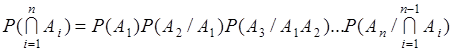 . (11.1)
. (11.1)
Рассмотрим важный частный случай формулы (11.1) для событий независимых в совокупности.
Определение. События 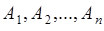 называются независимыми в совокупности, если события
называются независимыми в совокупности, если события 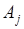 и
и 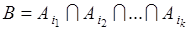 - независимые при любом выборе событий
- независимые при любом выборе событий 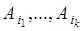 из данной совокупности и любом
из данной совокупности и любом 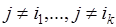 .
.
Для независимых 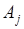 и
и 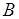 условные вероятности
условные вероятности 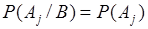 и формула (11.1) принимает вид
и формула (11.1) принимает вид
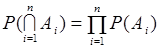 . (11.2)
. (11.2)
Отметим, что из независимости событий в совокупности следует их парная независимость. Но обратное утверждение неверно. Рассмотрим этот факт на примере Бернштейна. Пусть три грани правильного тетраэдра окрашены соответственно в красный (  ), зеленый (
), зеленый ( 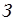 ) и синий (
) и синий ( 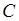 ) цвета, а четвертая - в три цвета (
) цвета, а четвертая - в три цвета (  ). Вероятность упасть тетраэдру гранью, на который есть, например, красный цвет, равна
). Вероятность упасть тетраэдру гранью, на который есть, например, красный цвет, равна 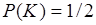 . Условная вероятность оказаться на этой грани красному цвету при условии, что на ней есть уже зеленый равна
. Условная вероятность оказаться на этой грани красному цвету при условии, что на ней есть уже зеленый равна 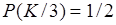 . Таким образом, события
. Таким образом, события 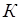 и
и 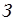 независимы. Аналогично, рассматривая любую пару событий, несложно определить, что события
независимы. Аналогично, рассматривая любую пару событий, несложно определить, что события 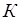 ,
, 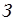 и С попарно независимы. Однако вероятность упасть гранью, на которой есть все три цвета равна
и С попарно независимы. Однако вероятность упасть гранью, на которой есть все три цвета равна 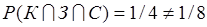 . Отсюда следует, что события
. Отсюда следует, что события 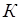 ,
, 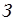 и С не являются независимыми в совокупности.
и С не являются независимыми в совокупности.
Рассмотрим примеры решения задач с использованием формул сложения и умножения вероятностей.
Определить вероятность разрыва цепочки из 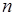 параллельно соединенных элементов, если вероятность разрыва в каждом элементе одинакова и равна
параллельно соединенных элементов, если вероятность разрыва в каждом элементе одинакова и равна 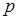 . Разрыв цепочки из
. Разрыв цепочки из 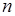 параллельных элементов означает наступление каждого из независимых в совокупности событий
параллельных элементов означает наступление каждого из независимых в совокупности событий 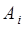 ,
,  ,
, 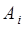 - разрыв
- разрыв 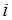 -го элемента. Таким образом, необходимо определить
-го элемента. Таким образом, необходимо определить  . Согласно формуле (11.2)
. Согласно формуле (11.2)
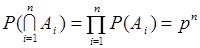 .
.  (11.3)
(11.3)
Определить вероятность разрыва цепочки из 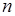 последовательно соединенных элементов, если вероятность разрыва в каждом элементе одинакова и равна
последовательно соединенных элементов, если вероятность разрыва в каждом элементе одинакова и равна 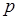 . В данном случае разрыв цепочки означает наступление хотя бы одного из независимых в совокупности событий
. В данном случае разрыв цепочки означает наступление хотя бы одного из независимых в совокупности событий 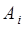 ,
,  . Следовательно, необходимо определить
. Следовательно, необходимо определить 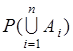 . Для этого можно воспользоваться формулой (10.1). Однако более простой путь получения решения - это вычисление через дополнительное событие
. Для этого можно воспользоваться формулой (10.1). Однако более простой путь получения решения - это вычисление через дополнительное событие 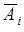 , которое состоит в том, что
, которое состоит в том, что 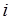 -й элемент остается в рабочем состоянии. Очевидно
-й элемент остается в рабочем состоянии. Очевидно 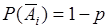 , откуда
, откуда 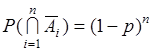 - вероятность того, что каждый элемент в рабочем состоянии. Следовательно, вероятность выхода из строя хотя бы одного элемента
- вероятность того, что каждый элемент в рабочем состоянии. Следовательно, вероятность выхода из строя хотя бы одного элемента
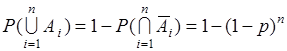 . (11.4)
. (11.4)
Представляет интерес сравнения результатов (11.3) и (11.4). Например, при  и
и  получаем
получаем 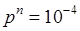 и
и 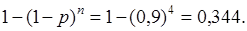
 2020-01-15
2020-01-15 139
139








