14.1 В общей теоретико-вероятностной схеме для каждого эксперимента со случайным исходом должны быть указаны все элементарные исходы, удовлетворяющие двум условиям: 1) в результате эксперимента происходит один и только один из этих исходов, 2) по смыслу элементарный исход неразложим на «более элементарные». Каждый такой исход принято называть элементарным событием и обозначать символом 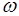 . Рассмотрим примеры элементарных исходов.
. Рассмотрим примеры элементарных исходов.
1. В опыте с бросанием монеты элементарными событиями являются: 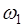 - выпадение герба,
- выпадение герба, 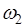 - выпадение «решетки». При этом считается, что стать на ребро монета не может.
- выпадение «решетки». При этом считается, что стать на ребро монета не может.
2. В эксперименте с игральной костью элементарные события 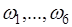 - это появление грани соответственно с номерами 1,...,6.
- это появление грани соответственно с номерами 1,...,6.
3. Последовательность из 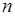 бросаний монеты. Здесь элементарными событиями являются последовательности вида:
бросаний монеты. Здесь элементарными событиями являются последовательности вида: 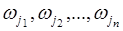 , где
, где 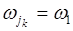 - появление герба или
- появление герба или 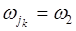 - появление «решетки». Число элементарных событий (разных последовательностей) равно
- появление «решетки». Число элементарных событий (разных последовательностей) равно  .
.
4. В эксперименте с бросанием точки на отрезок 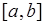 элементарное событие - это попадание точки в некоторую координату отрезка
элементарное событие - это попадание точки в некоторую координату отрезка 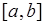 , что принято изображать точкой, расположенной в данной координате отрезка
, что принято изображать точкой, расположенной в данной координате отрезка 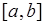 . Поэтому говорят, что элементарное событие в данном случае - это точка отрезка
. Поэтому говорят, что элементарное событие в данном случае - это точка отрезка 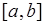 .
.
5. В эксперименте с бросанием двух точек на отрезок 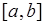 элементарное событие - это пара точек на
элементарное событие - это пара точек на 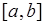 или одна точка в квадрате
или одна точка в квадрате 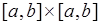 .
.
14.2. Множество всех элементарных событий в теории вероятностей принято называть пространством элементарных событий и обозначать буквой 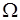 . Элементарные события
. Элементарные события 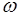 называют точками пространства элементарных событий
называют точками пространства элементарных событий 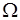 .
.
14.3. Всякий результат эксперимента со случайным исходом принято называть событием. Для каждого события 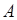 и каждого элементарного события
и каждого элементарного события 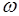 известно, влечет
известно, влечет 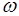 наступление
наступление 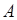 или нет, т.е. выполняется условие
или нет, т.е. выполняется условие 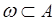 или нет. Тем самым совокупность тех
или нет. Тем самым совокупность тех 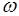 , которые влекут
, которые влекут 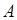 , полностью определяют
, полностью определяют 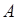 . Обратно: произвольное множество
. Обратно: произвольное множество 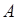 точек
точек 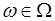 можно рассматривать как событие
можно рассматривать как событие 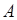 , которое происходит или нет в зависимости от того, принадлежит или нет множеству
, которое происходит или нет в зависимости от того, принадлежит или нет множеству 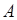 элементарное событие
элементарное событие 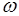 , представляющее данный исход опыта. Таким образом, событие
, представляющее данный исход опыта. Таким образом, событие 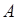 можно считать подмножеством
можно считать подмножеством 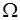 , состоящим из точек
, состоящим из точек 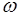 , представляющих те исходы эксперимента, при которых происходит
, представляющих те исходы эксперимента, при которых происходит 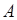 . По этой причине нет различия между событием
. По этой причине нет различия между событием 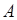 и соответствующим подмножеством
и соответствующим подмножеством 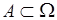 .
.
14.4. Рассмотрим примеры пространств элементарных событий. 1). В эксперименте с бросанием монеты пространство элементарных событий 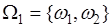 , где
, где 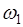 - появление герба,
- появление герба, 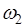 - появление «решетки». 2). При бросании игральной кости пространство элементарных событий
- появление «решетки». 2). При бросании игральной кости пространство элементарных событий 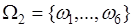 , где
, где 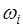 - выпадение грани с номером
- выпадение грани с номером 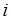 . 3). Если опыт состоит в бросании монеты
. 3). Если опыт состоит в бросании монеты 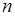 раз, то пространство элементарных событий
раз, то пространство элементарных событий 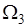 состоит из всех последовательностей вида
состоит из всех последовательностей вида 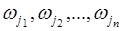 , где
, где 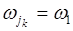 - появление герба или
- появление герба или 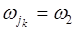 - появление «решетки». Число всех последовательностей (или точек пространства) равно
- появление «решетки». Число всех последовательностей (или точек пространства) равно 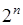 . 4). В опыте с бросанием точки на отрезок
. 4). В опыте с бросанием точки на отрезок 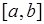 пространство элементарных событий
пространство элементарных событий 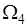 - это отрезок
- это отрезок 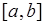 . 5). Наконец, при бросании двух точек на отрезок
. 5). Наконец, при бросании двух точек на отрезок 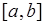 пространство элементарных событий
пространство элементарных событий 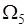 - это квадрат
- это квадрат 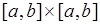 .
.
 2020-01-15
2020-01-15 111
111








