Объединение первых двух событий системы (8.1) 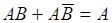 . В последовательности из
. В последовательности из 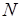 опытов событие
опытов событие 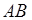 появилось
появилось 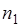 раз, а событие
раз, а событие 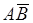 -
- 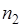 раз. Поэтому событие
раз. Поэтому событие 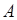 появилось
появилось 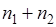 раз. Определим число появлений события
раз. Определим число появлений события 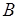 при условии, что событие
при условии, что событие 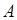 произошло. Событие
произошло. Событие 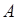 происходит, если происходит
происходит, если происходит 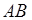 или
или 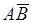 , число таких исходов равно
, число таких исходов равно 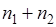 , при этом событие
, при этом событие 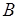 происходит, если происходит
происходит, если происходит 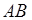 , число таких исходов равно
, число таких исходов равно 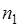 . Таким образом, условная частота появления события
. Таким образом, условная частота появления события 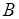 при условии, что
при условии, что 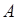 произошло
произошло
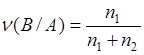 . (9.1)
. (9.1)
Из соотношений (8.3), (8.4), (9.1) следует:
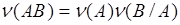 (9.2)
(9.2)
- формула умножения частот.
Эту формулу можно получить в другом виде. Аналогично (9.1)
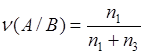 , (9.3)
, (9.3)
поскольку событие 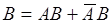 и появляется
и появляется 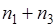 раз в последовательности из
раз в последовательности из 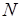 опытов, при этом событие
опытов, при этом событие 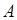 происходит
происходит 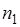 раз. Из соотношений (9.3) и (8.3), (8.5) следует:
раз. Из соотношений (9.3) и (8.3), (8.5) следует:
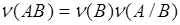 (9.4)
(9.4)
- второй вариант формулы умножения частот.
Поэтому в аксиомах теории вероятностей должна быть определена, или получена как следствие аксиом, формула умножения вероятностей:
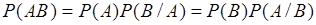 . (9.5)
. (9.5)
Если события 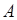 и
и 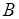 независимые, то условные вероятности равны безусловным:
независимые, то условные вероятности равны безусловным: 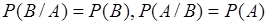 , тогда (9.5) принимает вид:
, тогда (9.5) принимает вид:
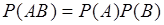 . (9.6)
. (9.6)
Обобщение формулы сложения вероятностей
Равенство (8.9) несложно обобщить на случай произвольного конечного числа событий. Вероятность того, что произойдет хотя бы одно из событий 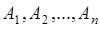 равна
равна
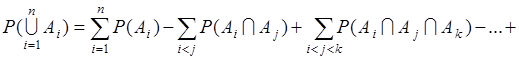
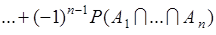 . (10.1)
. (10.1)
Здесь, например 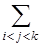 , означает тройную сумму по индексам
, означает тройную сумму по индексам 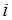 ,
, 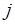 и
и 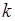 , которые пробегают значения
, которые пробегают значения 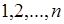 и удовлетворяют условию
и удовлетворяют условию  . Это условие приводит к уменьшению числа слагаемых тройной суммы по сравнению с числом
. Это условие приводит к уменьшению числа слагаемых тройной суммы по сравнению с числом 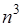 слагаемых в тройной сумме без ограничений на индексы суммирования. Последнее слагаемое (10.1) можно также рассматривать как
слагаемых в тройной сумме без ограничений на индексы суммирования. Последнее слагаемое (10.1) можно также рассматривать как 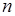 - кратную сумму по индексам
- кратную сумму по индексам 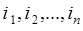 при условии на индексы:
при условии на индексы: 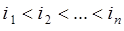 , что и приводит к вырождению
, что и приводит к вырождению 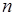 - кратной суммы до одного слагаемого (10.1).
- кратной суммы до одного слагаемого (10.1).
Пусть события 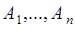 являются несовместными, тогда из (10.1) следует
являются несовместными, тогда из (10.1) следует
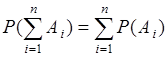 (10.2)
(10.2)
- вероятность суммы несовместных событий равна сумме их вероятностей.
 2020-01-15
2020-01-15 131
131








