Аксиомы теории вероятностей

Пусть  - пространство элементарных событий,  - алгебра событий (алгебра подмножеств множества 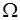). В основании теории вероятностей лежат следующие пять аксиом.

1. Алгебра событий  является - алгеброй событий.

Система событий  называется - алгеброй, если для всякой последовательности событий , , их объединение , пересечение  и дополнения , также принадлежат , т.е. , ,  являются также событиями. Таким образом, - алгебра  - это система событий, замкнутая относительно операций дополнения, счетного объединения и счетного пересечения.

2. На - алгебре событий  для любого  определяется функция , называемая вероятностью и принимающая числовые значения из интервала [0,1]: .

Данная аксиома - это аксиома существования вероятности  - как функции на  со значениями из интервала . Следующие три аксиомы определяют свойства функции .

3. Для любых двух событий , таких, что

                                  (15.1)

- аксиома сложения вероятностей.

Отсюда следует, что для конечного числа несовместных событий

    .                    (15.2)

4. Пусть , , - попарно несовместные события:  и пусть . Тогда

    .                                         (15.3)

Соотношение (15.3) называется аксиомой счетной аддитивности вероятности или аксиомой непрерывности вероятности. Второе связано со следующей интерпретацией равенства (15.3). Событие  следует понимать как предел последовательности

    .                                      (15.4)

При этом равенство (15.3) можно понимать как свойство непрерывности функции :  или

                        (15.5)

- которое позволяет операцию предела вынести за функцию . Это обусловлено тем, что из условия (15.5) следует (15.3):

.    (15.6)

5. .                                   (15.7)

Пятая аксиома указывает на то, что пространство элементарных событий 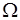 - есть достоверное событие. Таким образом,  содержит в себе все события, которые можно рассматривать в данной задаче.

Пространство элементарных событий , - алгебра событий  и вероятность  на , удовлетворяющие аксиомам 1-5, образуют так называемое вероятностное пространство, которое принято обозначать .

Отметим, что система аксиом 1-5 не противоречива, так как существуют , удовлетворяющие этим аксиомам и не полна, так как вероятность  можно определить многими способами в рамках аксиом 2-5. Понятие вероятностного пространства (или система аксиом 1-5) содержит лишь самые общие требования, предъявляемые к математической модели случайного явления, и не определяет вероятность однозначно. Последнее возможно только с учетом дополнительных условий, заданных в постановке рассматриваемой задачи.