Корреляционная функция случайного синхронного телеграфного биполярного сигнала с единичной высотой импульсов имеет следующий вид (рисунок 4):
 , (24)
, (24)
где 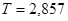 мкс=
мкс= 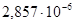 с.
с.
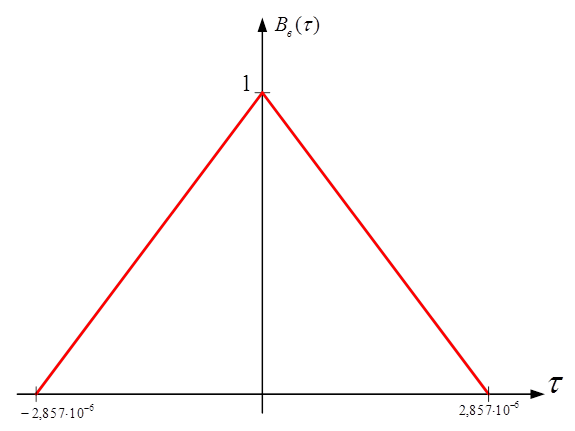
Рисунок 4 – График корреляционной функции модулирующего сигнала
Спектральная плотность мощности модулирующего сигнала
Для нахождения спектральной плотности мощности 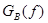 сигнала
сигнала 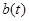 необходимо воспользоваться теоремой Хинчина-Винера, которая устанавливает связь между энергетическим спектром корреляционной функцией случайного процесса.
необходимо воспользоваться теоремой Хинчина-Винера, которая устанавливает связь между энергетическим спектром корреляционной функцией случайного процесса.
Спектральная плотность мощности модулирующего сигнала 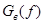 :
:
 (25)
(25)
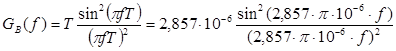 ,В2/Гц
,В2/Гц
График спектральная плотность мощности модулирующего сигнала представлен на рисунке 5.
| |


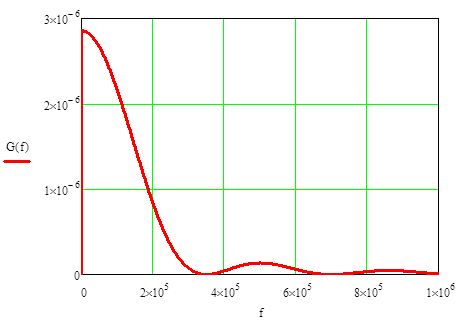
Рисунок 5 - График спектральная плотность мощности модулирующего сигнала
Условная ширина энергетического спектра модулирующего сигнала
Условная ширина энергетического спектра модулирующего сигнала найдем из условия
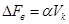 (26)
(26)
Пусть  1, тогда
1, тогда
 (Гц)=0,35 МГц
(Гц)=0,35 МГц
Определим долю мощности, сосредоточенную п полосе частот от 0 до 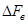 .
.
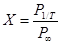 ;
; 


 (27)
(27)
Рассмотрим по отдельности числитель и знаменатель этого выражения.
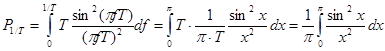
Возьмем этот интеграл по частям
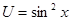 ;
;
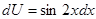 ;
;
 ;
;
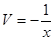 ;
;
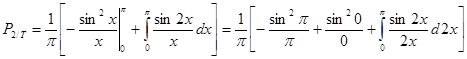
 - интегральный синус;
- интегральный синус;
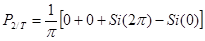 ;
;
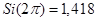 ;
;
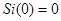
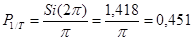
Аналогично получим,что 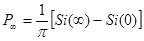 .
.
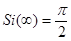 ;
; 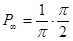 ;
;
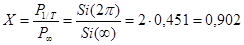
То есть получили, что 90,2% всей мощности сигнала приходится на полосу частот от 0 до  .
.
Энергетический спектр модулированного сигнала
Спектральная плотность мощности модулированного сигнала 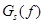 :
:
 (28)
(28)
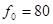 (МГц)
(МГц)
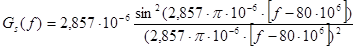
График спектральная плотность мощности модулированного сигнала представлен на рисунке 6.
Условная ширина энергетического спектра модулированного сигнала найдем из условия
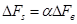 (29)
(29)
 (Гц)
(Гц)
| |




Рисунок 6 - График спектральная плотность мощности модулированного сигнала
Канал связи
Передача сигналов 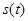 осуществляется по неискажающему каналу с постоянными параметрами и аддитивной флуктуационной помехой
осуществляется по неискажающему каналу с постоянными параметрами и аддитивной флуктуационной помехой  с равномерным энергетическим спектром
с равномерным энергетическим спектром 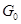 (белый шум).
(белый шум).
Сигнал на выходе такого канала можно записать следующим образом:
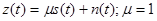
Требуется:
1. Определить мощность шума в полосе частот 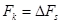 .
.
2. Найти отношение средней мощности сигнала к мощности шума.
3. Найти по формуле Шеннона пропускную способность канала в полосе  .
.
4. Определить эффективность использования пропускной способности канала 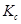 , определив ее как отношение производительности источника
, определив ее как отношение производительности источника 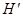 к пропускной способности канала
к пропускной способности канала 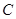 .
.
Мощность шума
В каналах связи аддитивные помехи возникают по различным причинам и могут принимать различные формы, индивидуальные реализации которых трудно учесть. Такие помехи чаще вызывают необратимые изменения передаваемых сигналов. Аддитивные помехи по своей структуре разделяют на три основных класса: распределенные по частоте и времени (флуктуационные), сосредоточенные по частоте (квазигармонические) и сосредоточенные во времени (импульсные).
Флуктуационные помехи порождаются в системах связи случайными отклонениями тех или иных физических величин (параметров) от их средних значений. Источником такого шума в электрических цепях могут быть флуктуации тока, обусловленные дискретной природой носителей зарядов.
Наиболее распространенной причиной шума в аппаратуре связи являются флуктуации, обусловленные тепловым движением.
Зная спектральную плотность мощности 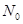 можно определить мощность шума
можно определить мощность шума 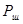 в полосе
в полосе  (промодулированного сигнала).
(промодулированного сигнала).
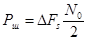 (30)
(30)
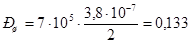 (В2)
(В2)
Для двоичных равновероятных символов 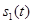 и
и 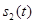 их средняя мощность будет равна:
их средняя мощность будет равна:
 (31)
(31)
где 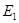 и
и 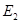 - энергия сигналов;
- энергия сигналов;
 - длительность сигналов.
- длительность сигналов.
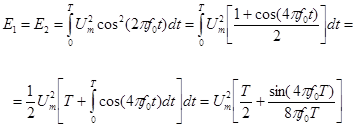 (32)
(32)
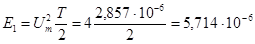
 (Дж)
(Дж)
При расчете мощности сигнала следует иметь в виду, что это понятие в технике связи имеет условный смысл. Физическая мощность согласно законам электротехники, конечно, зависит не только от сигнала (в форме напряжения или тока), но и от сопротивления нагрузки, на которой она выделяется. Под «мощностью сигнала» в связи условно принято понимать мощности, выделяемую на резисторе с сопротивлением 1 Ом.
Так как 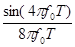 =0, то
=0, то
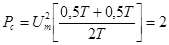 (В2)
(В2)
Но так как мы используем не всю мощность ее сигнала, а только 90,2% всей мощности, то
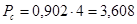 (В2)
(В2)
Отношение мощностей сигнала к мощности шума

 2020-01-15
2020-01-15 300
300








