Операции над нечеткими множествами

Для нечетких множеств, как и для обычных, определены основные операции: объединение, пересечение и инверсия/дополнение.

 Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:

Максиминные
Алгебраические
Ограниченные

Дополнение нечеткого множества во всех трех случаях определяется одинаково:

Пример. Пусть A — нечеткое множество "от 5 до 8"и B — нечеткое множество "около 4", заданные своими функциями принадлежности (рис.20):

Рис. 20. Функции принадлежности нечетких множеств А и B.

Тогда, используя максиминные операции, мы получим следующие множества, изображенные на рис. 21.

Рис. 21. Функции принадлежности нечетких множеств, полученных из А и B.

При максиминном и алгебраическом определении операций не будут выполняться законы противоречия и исключения третьего:

 

а в случае ограниченных операций не будут выполняться свойства идемпотентности и дистрибутивност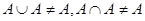и:

 и

Можно показать, что при любом построении операций объединения и пересечения в теории нечетких множеств приходится отбрасывать либо законы противоречия и исключения третьего, либо законы идемпотентности и дистрибутивности.

Нечеткая логика

Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.

Нечеткая переменная характеризуется тройкой <a, X, A>, где a - наименование переменной, X - универсальное множество (область определения a),
A - нечеткое множество на X, описывающее ограничения (т.е. m _A(x)) на значения нечеткой переменной a.

Лингвистической переменной называется набор <b,T,X,G,M>, где b - наименование лингвистической переменной, Т - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X (множество T называется базовым терм-множеством лингвистической переменной), G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения), М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.

Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый" и др. Ясно, что переменная "возраст" будет обычной переменной, если ее значения — точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.

Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению "молодой" может соответствовать функция принадлежности, изображенная на рис.22.

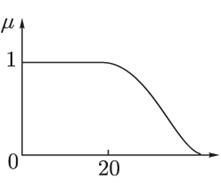
Рис.22. Функция принадлежности значения «молодой» лингвистической переменной «возраст»

Пример: Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий " малая толщина ", " средняя толщина " и " большая толщина ", при этом минимальная толщина равна 10 мм, а максимальная - 80 мм (рис. 23).

Формализация такого описания может быть проведена с помощью следующей лингвистической переменной <b, T, X, G, M>, где

b - толщина изделия;
T - {" малая толщина ", " средняя толщина ", " большая толщина "};
X - [10, 80];
G - процедура образования новых термов с помощью связок " и ", " или " и модификаторов типа " очень ", " не ", " слегка " и др. Например: " малая или средняя толщина " (рис. 24), "очень малая толщина " и др.;
М - процедура задания на X = [10, 80] нечетких подмножеств А₁=" малая толщина ", А₂ = "средняя толщина ", А₃=" большая толщина ", а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов " и ", " или ", " не ", " очень ", " слегка " и др.

Наряду с рассмотренными выше базовыми значениями лингвистической переменной " толщина " (Т={" малая толщина ", " средняя толщина ", " большая толщина "}) возможны значения, зависящие от области определения Х. В данном случае значения лингвистической переменной "толщина изделия" могут быть определены как " около 20 мм ", " около 50 мм ", " около 70 мм ", т.е. в виде нечетких чисел.

Рис. 23. Функции принадлежности нечетких множеств:
"малая толщина" = А₁, " средняя толщина "= А₂, " большая толщина "= А₃.

Рис. 24. Функция принадлежности:
нечеткое множество " малая или средняя толщина " = А₁ÈА₁

Нечеткими высказываниями будем называть высказывания следующего вида:

1. Высказывание <b есть b'>, где b - наименование лингвистической переменной, b' - ее значение, которому соответствует нечеткое множество на универсальном множестве Х.
Например, высказывание < давление большое > предполагает, что лингвистической переменной «давление» придается значение «большое», для которого на универсальном множестве Х переменной «давление» определено соответствующее данному значению «большое» нечеткое множество.

2. Высказывание <b есть mb'>, где m - модификатор, которому соответствуют слова «очень», «более или менее», «много больше» и др. Например: < давление очень большое >, < скорость много больше средней > и др.

3. Составные высказывания, образованные из высказываний видов 1. и 2. и союзов " И ", " ИЛИ ", " ЕСЛИ.., ТО...", "ЕСЛИ.., ТО.., ИНАЧЕ ".

Основным правилом вывода в традиционной логике является правило modus ponens, согласно которому мы судим об истинности высказывания B по истинности высказываний A и  

Например, если A — высказывание "Иван в больнице", B — высказывание "Иван болен", то если истинны высказывания "Иван в больнице" и "Если Иван в больнице, то он болен", то истинно и высказывание "Иван болен".

Во многих привычных рассуждениях, однако, правило modus ponens используется не в точной, а в приближенной форме. Так, обычно мы знаем, что A истинно и что , где есть, в некотором смысле, приближение A. Тогда из мы можем сделать вывод о том, что B приближенно истинно.

Нечеткая импликация выражается в следующем виде:

 и

Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме "Если-то" и функции принадлежности для соответствующих лингвистических термов. При этом должны соблюдаться следующие условия:

Ÿ существует хотя бы одно правило для каждого лингвистического терма выходной переменной;

Ÿ для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечетких правил.

Для реализации логического вывода необходимо выполнить следующее:

1. Сопоставить факты с каждым из правил и определить степень соответствия, назначив текущую силой правил.

2. Для каждого правила, сила которого больше заданного порога вычислить достоверность левой части.

3. Для каждого правила с помощью оператора импликации вычислить достоверность правой части.

4. Для многих результатов, полученных по различным правилам, выбрать одно (усредненное)

Пример. Пусть есть некоторая система, например, реактор, описываемая тремя параметрами: температура, давление и расход рабочего вещества. Все показатели измеримы, и множество возможных значений известно. Также из опыта работы с системой известны некоторые правила, связывающие значения этих параметров. Предположим, что сломался датчик, измеряющий значение одного из параметров системы, но знать его показания необходимо хотя бы приблизительно. Тогда встает задача об отыскании этого неизвестного значения (пусть это будет давление) при известных показателях двух других параметров (температуры и расхода) и связи этих величин в виде следующих правил:

· если Температура низкая и Расход малый, то Давление низкое;

· если Температура средняя, то Давление среднее;

· если Температура высокая или Расход большой, то Давление высокое.

Температура, Давление и Расход — лингвистические переменные.

Температура. Универсум (множество возможных значений) — отрезок [0, 150]. Начальное множество термов { Высокая, Средняя, Низкая }. Функции принадлежности термов имеют следующий вид (рис. 25):

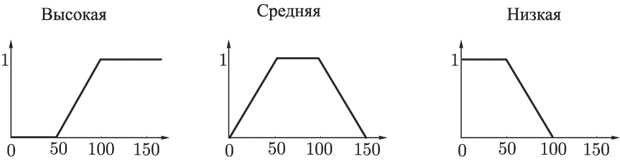
Рис.25. Функции принадлежности термов лингвистической переменной Температура

Давление. Универсум — отрезок [0, 100]. Начальное множество термов { Высокое, Среднее, Низкое }. Функции принадлежности термов имеют следующий вид (рис. 26):

Рис.26.  Функции принадлежности термов лингвистической переменной Давление

Расход. Универсум — отрезок [0, 8]. Начальное множество термов { Большой, Средний, Малый}. Функции принадлежности термов имеют следующий вид (рис. 27):

Рис.27. Функции принадлежности термов лингвистической переменной Расход

Пусть известны значения Температура - 85 и Расход - 3,5. Произведем расчет значения давления.

Этап фаззификации (переход от заданных четких значений к степеням уверенности). По заданным значениям входных параметров найдем степени уверенности простейших утверждений:

· Температура Высокая — 0,7;

· Температура Средняя — 1;

· Температура Низкая — 0,3;

· Расход Большой — 0;

· Расход Средний — 0,75;

· Расход Малый — 0,25.

Затем вычислим степени уверенности посылок правил:

· Температура низкая и Расход малый: min(Темп. Низкая, Расход Малый)= min(0.3, 0.25)=0.25;

· Температура Средняя: 1;

· Температура Высокая или Расход Большой: max(Темп. Высокая, Расход Большой)= max(0.7,0)=0,7.

Каждое из правил представляет из себя нечеткую импликацию. Степень уверенности посылки мы вычислили, а степень уверенности заключения задается функцией принадлежности соответствующего терма. Поэтому, используя один из способов построения нечеткой импликации, мы получим новую нечеткую переменную, соответствующую степени уверенности в значении выходных данных при применении к заданным входным соответствующего правила. Используя определение нечеткой импликации как минимума левой и правой частей (определение Мамдани), имеем (рис. 28):

Рис.28. Результат этапа фаззификации.

Этап аккумуляции (объединение результатов применения всех правил). Один из основных способов аккумуляции — построение максимума полученных функций принадлежности (объединение функций принадлежности, полученных на этапе фаззификации).

Полученную функцию принадлежности уже можно считать результатом. Это новый терм выходной переменной Давление. Его функция принадлежности говорит о степени уверенности в значении давления при заданных значениях входных параметров и использовании правил, определяющих соотношение входных и выходных переменных. Но обычно все-таки необходимо какое-то конкретное числовое значение.

 

Рис.29. Результат этапа аккумуляции.

Этап дефаззификации (получение конкретного значения из универса по заданной на нем функции принадлежности). Существует множество методов дефаззификации, но в этом случае достаточно метода первого максимума. Применяя его к полученной функции принадлежности, получаем, что значение давления — 50. Таким образом, если мы знаем, что температура равна 85, а расход рабочего вещества — 3,5, то можем сделать вывод, что давление в реакторе равно примерно 50.