При типовом воздействии

Исходным выражением для вычисления квадратичной интегральной оценки является передаточная функция замкнутой скорректированной системы по каналу х_з-ε при единичном ступенчатом воздействии (то есть принимаем задающее воздействие Х_з(t)=1, а следовательно Х_з(р)=1/р). Запишем эту передаточную функцию:

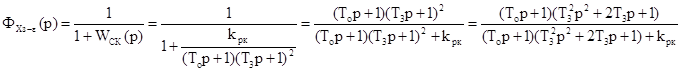
Раскроем скобки и приведем передаточную функцию к стандартному виду:

Подставим в формулу численные значения:

                      

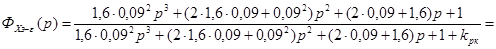
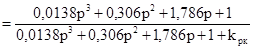
Запишем выражение для изображения переходной составляющей сигнала ошибки:

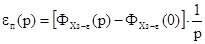
Так как передаточный коэффициент разомкнутого контура k_рк≥10 допускается упростить выражение для изображения переходной составляющей с учетом следующих условий:

k_рк+1=k_рк и k_рк-1=k_рк

Преобразуем выражение для изображения переходной составляющей сигнала ошибки, используя вышеприведенные условия:

     =

 

    

    

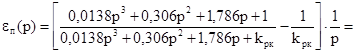
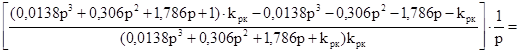
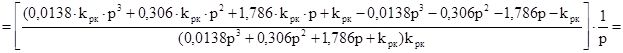
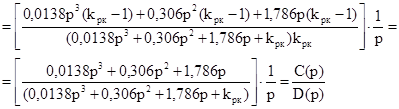
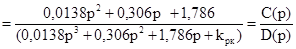
Для вычисления квадратичной оценки по изображению используют равенство Парсеваля, которое имеет вид:

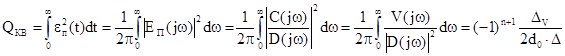
Где

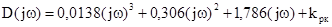
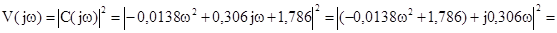
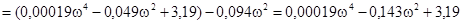
Таким образом коэффициенты d_i и v_i равны:

d_o =0,0138                  v_o =0,00019

d₁ =0,306                    v₁ =-0,143

d₂ =1,786                    v₂ =3,19

d₃ = k_рк

Составим определитель Δ по правилу составления определителя Гурвица

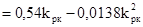
Определитель D_v составляем из определителя D путем замены коэффициентов верхней строки на коэффициенты n₀, n₁ и n₂.

Вычисляем квадратичную интегральную оценку:

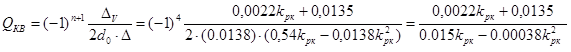
Задаваясь численными значениями k_рк, составляем таблицу зависимости квадратичной интегральной оценки от коэффициента k_рк, которая приведена ниже.

 

Таблица 5. – Расчетные данные для построения кривой зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

 

крк	Qкв
1	1.074
2	0.629
3	0.483
4	0.414
5	0.374
6	0.349
7	0.335
8	0.325
9	0.319
10	0.317
11	0.317
12	0.319
13	0.322
14	0.327
15	0.333
20	0.389
25	0.498
30	0.736
35	1.521

 

 

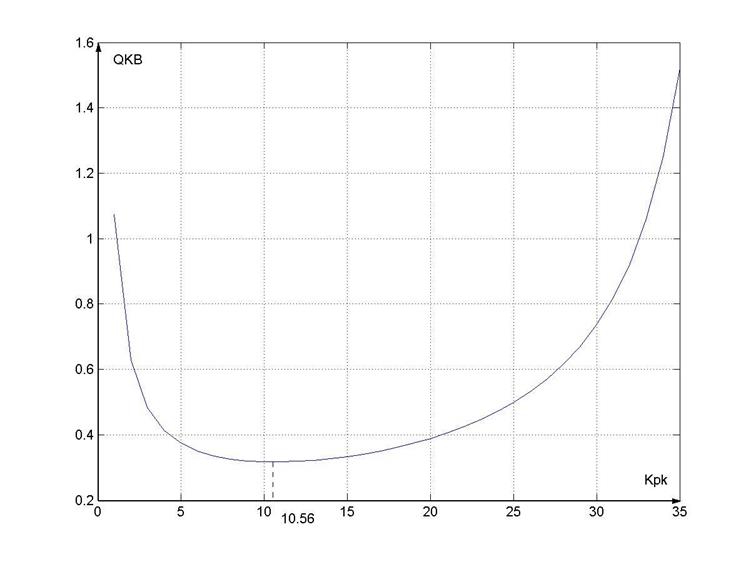
Рис. 9 - Кривая зависимости интегральной оценки от передаточного коэффициента разомкнутого контура

 

При помощи программы Matlab вычислим минимум функции Q_кв на интервале [1;35], он равен 10,56. Следовательно, оптимальным значением k_рк является k_рк=10,56. При данном значении коэффициента разомкнутого контура система будет работать в оптимальном режиме, обеспечивая минимальную площадь под графиком переходного процесса.

Теперь перейдем от коэффициента k_рк к передаточному коэффициенту k_у. Для этого воспользуемся следующей формулой:

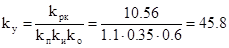
При коэффициенте k_рк=10,56 и квадратичной интегральной оценке равной Q=0.3166 передаточный коэффициент управляющего устройства k_у.= 45,8.

 

Вывод: В этом разделе с помощью квадратичной интегральной оценки получили оптимальное значение передаточного коэффициента управляющего устройства (k_у=45,8). Этот коэффициент получился меньше, чем тот, что был выбран в разделе 2 (k_у=56,3). Следовательно, при выборе этого коэффициента точность системы в установившемся режиме увеличится, но могут получиться более колебательные переходные процессы.