Исходным выражением для построения области устойчивости является характеристическое уравнение замкнутого контура скорректированной системы. Запишем это характеристическое уравнение:

Подставим в формулу выражение для передаточной функции разомкнутого контура.





Заменяем р на jω.

Объединим действительную и мнимую составляющие выражения:

Приравняем к нулю действительную и мнимую части:

Упорядочим систему уравнений относительно параметров kрк и To:

Решим эту систему уравнений методом Крамера.

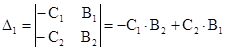



Подставим значения коэффициентов в выражения kрк и То .

= 


Так как область устойчивости надо строить в плоскости параметров kи и TО, то сделаем переход от коэффициента kрк к коэффициенту kи .
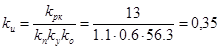
С учетом этого запишем уравнение kрк относительно нужного нам параметра kи .
kи = 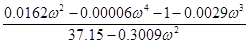
Задаваясь значениями частоты ω от 0 до ∞, составляем таблицу 2, получаем данные для построения границы области устойчивости системы в плоскости двух параметров kи и Tо .
Таблица 2. – Расчетные данные для построения границы области устойчивости системы
| ω | kи | To |
| 0 | -0.0269 | 0 |
| 1 | -0.0268 | -0.0163 |
| 2 | -0.0267 | -0.0335 |
| 3 | -0.0272 | -0.0524 |
| 4 | -0.0291 | -0.0744 |
| 5 | -0.0336 | -0.1016 |
| 6 | -0.0426 | -0.1372 |
| 7 | -0.0600 | -0.1880 |
| 8 | -0.0947 | -0.2691 |
| 9 | -0.1718 | -0.4240 |
| 10 | -0.4079 | -0.8526 |
| 11 | -5.0980 | -8.9548 |
| 12 | 0.7966 | 1.1683 |
| 13 | 0.4632 | 0.5709 |
| 14 | 0.3705 | 0.3860 |
| 15 | 0.3332 | 0.2954 |
| 20 | 0.3283 | 0.1446 |
| 25 | 0.3951 | 0.0997 |
| 30 | 0.4850 | 0.0773 |
| 35 | 0.5899 | 0.0635 |
| 40 | 0.7074 | 0.0542 |
| 45 | 0.8363 | 0.0473 |
| 50 | 0.9761 | 0.0421 |
| 55 | 1.1265 | 0/0379 |
Используя данные таблицы 2, построим область устойчивости скорректированной системы в плоскости двух параметров kи и Tо. Область устойчивости приведена на рисунке 5.

Рис. 5. - Область устойчивости скорректированной системы в плоскости двух параметров kи и Tо
Вывод: Как видно из рисунка 5 при коэффициенте kи =0,35 и постоянной времени То=1.6 система находится в области устойчивой работы, что означает правильность расчета корректирующего устройства. Таким образом, при заданных настройках системы автоматического регулирования, удовлетворяющих требованиям точности, система устойчива.
Построение графика переходного процесса и оценка качества
скорректированной системы
 2020-01-15
2020-01-15 128
128








