2020-01-15
138
В разделе 1.4 нами была получена модель термодинамических свойств системы Ni-Si, которая описывалась с помощью обобщенной теории "регулярных" растворов в однопараметрическом приближении. Проверяем адекватность полученной модели, решая обратную задачу: рассчитываем мольные доли компонентов раствора, задавая температуру, энергию Гиббса и рассчитанные нами энергии смешения Q12 по уравнениям (1.20) и (1.21). При этом экстраполируем зависимость до комнатных температур. На рис.2.1 точками обозначены исходные данные из диаграммы Ni-Si, а сплошной линией показана полученная модель.
Рис.2.1 Проверка адекватности модели.
Как видно из графика, при 00С растворимость Si в Ni составляет около 0,022 % (ат.).
2.2 Расчет активностей компонентов системы Ni-Si при 250С
В соответствии с обобщенной теорией "регулярных" растворов, активности компонентов двойной системы можно рассчитать по следующим уравнениям:
; (2.1)
; (2.2)
В рамках однопараметрического приближения теории "регулярных" растворов и непосредственно для системы Ni-Si эти уравнения перепишутся следующим образом:
,
.
Результаты расчетов предоставлены в таблице 2.4.
Таблица 2.4.
Состав и активности компонентов системы Ni-Si при 250С
| Компонент | xi | 
|
| Si | 0,0228 | 7,370*10-29 |
| Ni | 0,9772 | 0,9394 |
2.3 Расчет диаграммы состояния системы Ni-Si-O при 25 0С. Анализ химической устойчивости
Как следует из экспериментальных данных по системе никель-кремний (рис.1.1), никель-кислород (рис.1.3) и кремний-кислород (рис.1.4) схема фазовых равновесий в системе никель-кремний-кислород при 298 К и 1 атм. имеет вид (рис.2.2).
Рис.2.2 Фазовая диаграмма состояния системы Ni-Si-O при 25 0С.
Поскольку химическое сродство кремния к кислороду выше, чем никеля, то можно предположить, что почти при любом составе сплава Ni-Si в первую очередь будет реализовываться равновесие сплав - SiO2.
На диаграмме 2.2 можно выделить области, в которых присутствуют следующие фазы:
1. Si (γ) - NiSi2 - SiO2; (I)
2. NiSi2 - NiSi - SiO2; (II)
3. NiSi - Ni3Si2 - SiO2; (III)
4. Ni3Si2 - Ni2Si - SiO2; (IV)
5. Ni2Si - Ni3Si - SiO2; (V)
6. Ni3Si - γ-фаза - SiO2; (VI)
7. γ - фаза - Ni2SiO4 - NiO; (VII)
8. γ-фаза - Ni2SiO4 - NiO; (VIII)
9. Ni2SiO4 - NiOх, 1<x<1,346; (IX)
10. Ni2SiO4 - SiO2 - NiOx, 1,346<x<1,903; (XI)
Примеры расчета:
а) Фазовое равновесие VII:
γ-фаза - Ni2SiO4 - SiO2 было описано независимыми реакциями образования SiO2 и Ni2SiO4 из компонентов γ-фазы (Ni, Si) и компонентов газовой фазы O2:
(1) 
;
(2) 
;
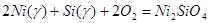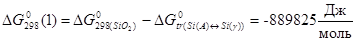
Константы равновесия реакций 1 и 2:
; (2.3), 
; (2.4)
Для определения состава γ-фазы исключим 
из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в квадрат и поделим полученное на уравнение (2.4), получим:
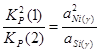; (2.5)
Это уравнение можно переписать в виде:
; (2.6)
Из уравнения изотермы химической реакции:
; (2.7)
уравнение (2.3.4) можно переписать:
; (2.8)
Данное трансцендентное уравнение можно решить только численным методом. Обозначив xSi=x, xNi=x-1, получим:
; (2.9)
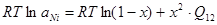; (2.10)
Подставив уравнения (2.9) и (2.10) в (2.8) решаем численным методом, находим значение х. Исходя из уравнений (2.3) или (2.4) определяем величину 
.
Для остальных трехфазных равновесий расчет производился тоже исходя из константы равновесия. Например, для равновесия IV:
Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:
; (2.11)
Результаты расчетов приведены в таблице 2.5.
Таблица 2.5.
Характеристики фазовых равновесий системы Ni-Si-O при 25 0С
| № | Равновесие |  , атм.
| Равновесный состав фаз |
| I | Si (γ) - NiSi2 - SiO2 | 1,07*10-156 | 
|
| II | NiSi2 - NiSi - SiO2 | 3,35*10-150 | 
|
| III | NiSi - Ni3Si2 - SiO2 | 1,48*10-144 | 
|
| IV | Ni3Si2 - Ni2Si - SiO2 | 2,00*10-135 | 
|
| V | Ni2Si - Ni3Si - SiO2 | 1,27*10-128 | 
|
| VI | Ni3Si - γ-фаза - SiO2 | 3,04*10-129 | 
|
| VII | γ - фаза - Ni2SiO4 - SiO2 | 2,44*10-81 | 
|
| VIII | γ - фаза - Ni2SiO4 - NiO | 8,68*10-75 | 
|
| IX | Ni2SiO4 - NiOх, 1<x<1,346 | 0,21 | 
|
| X | Ni2SiO4 - SiO2 - NiOx, 1,346<x<1,903 | 0,21 | 
|
| XI | NiO1,903 - NiO2 - SiO2 | 9,48*1030 | 
|
б) Расчет равновесия NiOx - Ni2SiO4 - SiO2
Окисление Ni2SiO4 на воздухе завершится образованием фазы NiOx. Для нахождения значения x решим уравнение:
; (2.12), 
; (2.13)
; (2.14)
Чтобы знать в явном виде зависимость 
от х воспользуемся функциональной зависимостью между стандартной энергией образования оксидов данного металла из элементов и стехиометрическим составом оксидов:
; (2.15),
где i, j - степени окисленности оксидов металла, для которых существуют наиболее достоверные термодинамические данные,
х - степень окисленности неизвестного оксида.
Наиболее достоверные термодинамические данные для никеля получены для оксида NiO:
Данные для оксида Ni2O3 получены расчетным путем: 
. Поскольку для гипотетического оксида NiO1,5 энергия Гиббса образования вдвое меньше, то 
. Таким образом, 
, 
, 
, i=1, j=1,5 и энергия Гиббса оксида NiOx:
; (2.16)
Подставляя (2.3.13) в (2.3.12) и полученное выражении для 
в (2.3.11), находим значение x, соответствующее максимальной степени окисленности никеля в оксиде, полученного окислением Ni2SiO4 на воздухе: х=1,903.
Из результатов расчета следует, что химическое сродство кремния к кислороду намного выше, чем у никеля. Вплоть до содержания кремния в γ - фазе - 10-40 моль единственной оксидной фазой (продуктов окисления сплава) является кремнезем. Окисление сплавов начинается при давлении кислорода большем чем 10-156 атм, поэтому сплавы будут окисляться кислородом воздуха при 250 С. Так как для образования NiO2 требуется давление кислорода в газовой фазе над сплавом большее, чем 9,48*1030, то при окислении сплавов кислородом воздуха NiO2 образовываться не будет. Окисления никеля завершится образованием фазы NiOx.
2.4 Расчет диаграммы состояния системы Ni-Si-H2O при 250С. Анализ химической устойчивости
Диаграммы рН-потенциал строят, зафиксировав активности компонентов, находящихся в растворе. В данной работе построены диаграммы рН-потенциал для системы Ni-Si-H2O при активностях ионов в растворе равных 1 
, 10-3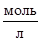 
, 10-6 . Они представлены соответственно на рис.2.3, 2.4, 2.5 Основные химические и электрохимические равновесия указаны в табл.2.6.
При построении диаграмм были использованы данные из табл.1.5 и табл.2.2-2.3. В качестве примера рассмотрим расчеты некоторых равновесий:
1) Электрохимическое равновесие 3:
рассчитывалось комбинацией следующих реакций:
а) 
,
;
б) 
,
В; Так как 
, (2.17)
то свободная энергия Гиббса электрохимической реакции (б) будет равна:
.
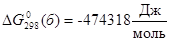По закону Гесса 
будет равна:
.
Согласно уравнению (2.17):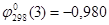 
В.
Таблица 2.6.
Основные химические и электрохимические равновесия в системе Ni-Si-H2O при 25 0С, 1 атм. (воздух)
| №линии | Электродная реакция | Равновесный потенциал (В) или рН раствора |
|  атм.
| 0,186-0,0591рН |
|  атм.
| 1,219-0,0591рН |
| 1 | 
| -1,151-0,0591рН |
| 2 | 
| 
|
| 3 |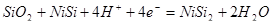 
| -0,980-0,0591рН |
| 4 | 
| 
|
| 5 | 
| -0,897-0,0591рН |
| 6 | 
| 
|
| 7 | 
| -0,762-0,0591рН |
| 8 |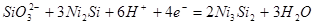 
| 
|
| 9 |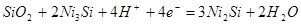 
| -0,714-0,0591рН |
| 10 |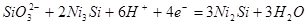 
| 
|
| 11 | 
| -0,645-0,0591рН |
| 12 | 
| 
|
| 13 | 
| рН 
|
| 14 | 
| 
|
| 15 | 
| -0,49-0,0591рН |
| 16 | 
| 0,133-0,0591рН |
| 17 | 
| 
|
| 18 | 
| рН 3,4 |
| 19 | 
| (0,806х2-0,67х-0,0591хрН) / (х-1) |
| 20 | 
| 1,602-0,0591рН |
| 21 | 
| 
|
| 22 | 
| 
|
Подставив значение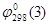 
в уравнение (1.27) или (1.28) и учитывая, что 
, получим равновесный потенциал реакции (3):
рН.
2) Электрохимическое равновесие 4:
рассчитывалось сложением равновесий 3 и 13:
а) 
,
;
б) 
, рН 13,94.
Используя уравнение (1.31), найдем энергию Гиббса реакции (б):
.
Тогда энергия Гиббса равновесия 4:
,
Отсюда 
.
Равновесный потенциал реакции 4:
Аналогичным образом были рассчитаны остальные фазовые равновесия. Результаты расчетов приведены в табл.2.6.
Рис.2.3 Диаграмма рН-потенциал системы Ni-Si-H2O при 25 0С, 1 атм. (воздух) и 
=1 .
Рис.2.4 Диаграмма рН-потенциал системы Ni-Si-H2O при 25 0С, 1 атм. (воздух) и 
=10-3 
.
Рис.2.5 Диаграмма рН-потенциал системы Ni-Si-H2O при 25 0С, 1 атм. (воздух) и =10-6 .
На диаграмме можно выделить 21 область преобладания различных фаз:
I. 
II.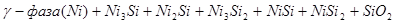 
III. 
IV. 
V.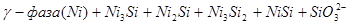 
VI. 
VII. 
VIII. 
IX.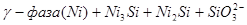 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
XVII. 
XVIII. 
XIX. 
XX. 
XXI. 
Область I - область иммунности γ-фазы, интерметаллидов и чистого кремния, когда сплав не подвергается коррозии. Выше линии 1 кремний термодинамически неустойчив и окисляется до кремнезема (
) в кислых средах и до 
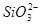в щелочных средах, интерметаллиды и γ-фаза остаются термодинамически устойчивыми фазами. Выше линии 3 происходит последовательное диспропорционирование 
, 
и так далее вплоть до 
. Области XIV, XVI и XVII - области термодинамической устойчивости 
. В кислых средах он неустойчив и распадается с образованием 
и свободных ионов никеля 
. Области XVII, XVIII и XIX отвечают образованию оксидов никеля 
. В областях транспассивности - XX и XXI - происходит перепассивация сплава по никелю. Коррозия сплава происходит во всех областях, находящихся правее линии 13, а также избирательная коррозия в областях XV и XVI.
Состав образующейся пассивационной пленки может быть разным. Если в сплаве достаточно много кремния, то образуется сплошная пассивационная оксидная пленка в виде . Если кремния недостаточно для образования сплошной пленки из кремнезема, пассивационная пленка представляет из себя 
. В случае недостатка кремния даже для образования , в качестве пассивационной пленки выступает оксид никеля с включениями из . Сравнение диаграмм, построенных при различных значениях активностей ионов в растворе, показывает, что с уменьшением активностей ионов снижаются потенциалы растворения компонентов сплава и потенциал перепассивации сплава по никелю. Области активной коррозии расширяются, а области пассивности наоборот уменьшаются и сдвигаются в более кислую область. Области устойчивости XIV и XVI тоже имеют тенденцию к уменьшению. Линии 
и 
на диаграммах (рис.2.3-2.5) определяют электрохимическое поведение воды (см. табл.2.5). В области ниже линии 
происходит катодное восстановление воды с выделением водорода. Область между линиями 
и определяет электрохимическую устойчивость воды. Выше линии происходит окисление воды с выделением кислорода на аноде.
