Показательная зависимость имеет вид
 (6)
(6)
Во всех случаях  при
при  . Если
. Если  то при
то при  кривая растет с увеличением
кривая растет с увеличением 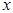 тем быстрее, чем больше
тем быстрее, чем больше 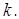 При
При  она приближается к оси абсцисс с возрастанием
она приближается к оси абсцисс с возрастанием 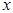 тем быстрее, чем больше абсолютная величина
тем быстрее, чем больше абсолютная величина 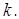
Если найденная на опыте зависимость  от
от 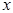 является показательной, то график зависимости
является показательной, то график зависимости 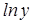 от
от 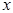 представляет собой прямую линию, тангенс угла наклона которой равен параметру
представляет собой прямую линию, тангенс угла наклона которой равен параметру 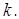 Если значение
Если значение  при
при  неизвестно, то величину параметра
неизвестно, то величину параметра 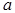 можно найти по формуле
можно найти по формуле  для ряда значений
для ряда значений 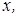 а затем взять среднее.
а затем взять среднее.
Рисунок 2 График показательной функции
Найдем коэффициенты  и
и 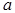 для исходной таблицы 1, если известно, что приближающую функцию целесообразно искать в виде показательной функции (6).
для исходной таблицы 1, если известно, что приближающую функцию целесообразно искать в виде показательной функции (6).
Прологарифмируем равенство (6):
 (7)
(7)
приняв обозначения  перепишем (7) в виде:
перепишем (7) в виде:
 (8)
(8)
Таким образом приближающая показательная функция нехитрыми преобразованиями сведена к линейной, следовательно, для определения коэффициентов 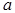 и
и  показательной функции можно воспользоваться выведенной для линейной функции формулой
показательной функции можно воспользоваться выведенной для линейной функции формулой
 (9)
(9)
Итак, для нахождения приближающей функции в виде (6) нужно прологарифмировать значения функции в исходной таблице 1 и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы 3 приближающую функцию вида (8).
Таблица 1 Таблица 3

| 
|
Окончательно получаем:
 (9)
(9)

Рисунок 3 – График логарифмической функции
Замечание: формулам
 (10)
(10)
 (11)
(11)
соответствуют кривые, изображенные на рисунках 1 и 2, сдвинутые вверх или вниз на величину  . Например, кривая, изображенная на рисунке 3, соответствует формуле
. Например, кривая, изображенная на рисунке 3, соответствует формуле  при
при  и
и  Чтобы найти параметры этих формул, следует сначала определить значение
Чтобы найти параметры этих формул, следует сначала определить значение  Иногда величину
Иногда величину  можно легко найти по значению, к которому стремится
можно легко найти по значению, к которому стремится  при возрастании
при возрастании  (при
(при  ) или по значению
) или по значению  при
при  (для формулы 10 при
(для формулы 10 при  ). Можно также воспользоваться формулой
). Можно также воспользоваться формулой

где  и
и  — ординаты произвольных (но достаточно далеких) точек с абсциссами
— ординаты произвольных (но достаточно далеких) точек с абсциссами 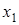 ,
, 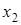 , а ордината
, а ордината  соответствует абсциссе
соответствует абсциссе  в случае формулы (10) и абсциссе
в случае формулы (10) и абсциссе 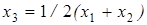 в случае формулы (11).
в случае формулы (11).
3.3. Логарифмическая функция
Будем искать приближающую функцию в виде
 (12)
(12)
Для перехода к линейной функции достаточно выполнить подстановку 
Отсюда следует, что для нахождения значений a и b нужно прологарифмировать значения аргумента в исходной таблице 1 и для новой таблицы 4 найти приближающую функцию в виде линейной y=at+b. Коэффициенты a и b найденной функции подставить в формулу 2.14.

| 
|
| Таблица 4 | Таблица 5 |
Окончательно получим:

(13)
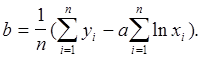

Рисунок 4 График логарифмической функции
 2020-01-15
2020-01-15 432
432








