Понятие состояния системы

Свойства системы S в конкретные моменты времени называются состояниями. Процесс функционирования системы во времени можно рассматривать как последовательную смену состояний системы z₁(t), z₂(t),… z_k(t). Совокупность всех возможных состояний 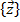называется пространством состояний Z объекта моделирования, причем z_k € Z.

Состояние системы S в произвольный момент времени t₀<t^*≤T полностью определяется начальным состоянием , где , а также входными воздействиями , внутренними параметрами 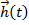, воздействием внешней среды на интервале времени (t^* - t₀) с помощью векторных уравнений (2) и (3).

Соотношение (2) позволяет определить состояние системы в текущий момент времени по начальному состоянию системы и по экзогенным переменным.

(2)

Соотношение (3) позволяет определить выходные характеристики системы (эндогенные переменные) по её состоянию.

(3)

Соотношение (4) – это уравнение в общем виде для определения выходных характеристик системы.

(4)

Время в модели системы S может рассматриваться на интервале моделирования (0,T) как в непрерывной, так и в дискретной форме, т.е. в виде квантов длиной t, где m – число интервалов дискретизации (соотношение (5)).