Цель работы с точки зрения математики:
• расширение и углубление знаний по вопросам исследования функций и
построения их графиков;
• развитие самостоятельности при работе с методическим материалом;
• привитие понимания единства математических методов решения задач
(моделирование, алгоритмизация);
• формирование умений перехода от одной формы представления
математических фактов к другой, что способствует повышению качества
усвоения знаний.
План работы по математической составляющей задания:
1) область определения функции;
2) четность;
3) непрерывность, вертикальные асимптоты;
4) точки пересечения с осями;
5) точки экстремума и монотонность;
6) наклонные асимптоты, поведение функции при 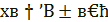 ;
;
7) график.
Задания подбираются так, чтобы в зависимости от значения параметра график функции имел или не имел точки разрыва, т. е. функция обладала бы различными свойствами в зависимости от параметра. Такая вариативность способствует развитию гибкости мышления.
Цель работы с точки зрения информатики:
• изучение основных возможностей графического модуля программной
среды;
• закрепление знаний учащихся по преобразованию типов данных;
• формирование некоторых элементов компьютерной грамотности учащихся (написание и оформление программы с учетом требований к графическому интерфейсу).
План написания программы: 1) ввод входных параметров; 2)построение графика функции.
Конспект урока 1 (2часа)
Тема: «Показательная функция»
Цели урока:
Образовательные:
• знать общую схему и особенности проведения исследования функций;
• уметь проводить формализацию задачи.
Воспитательная:
• воспитание трудолюбия.
Развивающие:
• развитие познавательного интереса;
• развитие самостоятельности при работе с методическим материалом;
• формирование информационной культуры.
Методы обучения:
1. Практическая работа.
План урока:
1. Организационный момент (2 мин)
2. Объявление целей урока (2 мин)
3. Практическая работа (30 мин)
4. Самостоятельная работа (40 мин)
5. Подведение итогов (6 мин)
Ход урока отображен в табл. 6.
Таблица 6.
Ход урока
| Учитель | Ученики | Тетрадь |
| Здравствуйте. Садитесь. | Здравствуйте. | |
| Тема нашего сегодняшнего урока «Исследование функций. Показательная функция». | Исследование функций. Показательная функция | |
Первый урок будет посвящен повторению этапов исследования функций на примере функции  , после чего на втором уроке вы должны будете уже самостоятельно исследовать показательные функции. , после чего на втором уроке вы должны будете уже самостоятельно исследовать показательные функции.
| ||
| Сейчас я вам выдам раздаточный материал, в котором подробно описан ход решения задачи. Внимательно изучите и поэтапно выполните то, что от вас требуется. Если кто-то выполняет задание раньше, он может приступать к задачам для самостоятельного решения, которые приведены в конце раздаточного материала. | Ученики берут раздаточный материал, садятся за компьютеры и начинают работать. | Пример
Исследование функции 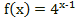 .
1. .
1. 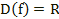 2.
2.  следовательно, f(x) является функцией общего вида.
3. Функция непрерывна в D(f). Точек разрыва нет и нет вертикальных асимптот.
4. Если х = 0, то следовательно, f(x) является функцией общего вида.
3. Функция непрерывна в D(f). Точек разрыва нет и нет вертикальных асимптот.
4. Если х = 0, то  т. е. (0; т. е. (0; 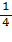 ) - точка пересечения с ) - точка пересечения с
|
| Учитель | Ученики | Тетрадь |
| осью OY. | ||
| 5. у = 4х-1ln4>0 при любых | ||
| xєR. | ||
| Значит, f(x) возрастает на всей | ||
| области определения. | ||
| yn= (4x-1ln 4)' = 4x-1 In2 4 > 0 при | ||
| всехх | ||
| Значит, выпуклость графика | ||
| направлена вниз на всей | ||
| области определения. | ||
| Конец первого урока. | ||
| Все справились? (Подходит к | Нет. | |
| тем, кто не успел и ищет | ||
| ошибку, указывает на нее, но | ||
| не исправляет.) | ||
| Все успели? | Да. | |
| Начало второго урока. | (Делают | |
| Переходим к решению | самостоятельно.) | |
| самостоятельных задач. | ||
| Внимательно ознакомьтесь и | ||
| приступайте к решению. При | ||
| затруднениях поднимайте | ||
| руку, я подойду. | ||
| И так все успели? Сейчас я | Да. | |
| подойду к каждому и | ||
| проверю решение. | ||
| Нет. | ||
| У вас еще остались вопросы | ||
| по пройденной теме? | ||
| Следующая тема будет | ||
| «Исследование | ||
| логарифмической функции». | ||
| В ней вам нужно будет | ||
| применять знания, которые | ||
| мы получили на | ||
| сегодняшнем уроке. Кто не | ||
| успел решить задачи на | ||
| уроке, должен будет их | ||
| доделать дома. |
Раздаточный материал
«Исследование функций. Показательная функция» Пример
Исследование функции f(x) = 4x-1.
1. D(f) = R
2.  следовательно, f(x) является функцией
следовательно, f(x) является функцией
общего вида.
3. Функция непрерывна в D(f)
Точек разрыва нет и нет вертикальных асимптот.
Если х = 0, то у =  , т. е. (0;
, т. е. (0;  ) - точка пересечения с осью OY
) - точка пересечения с осью OY
4. у' = 4x-1ln4 > 0 при любых хєR.
Значит, f(x) возрастает на всей области определения.
у" = (4x-1ln4) = 4x-1ln24 > 0 при всех х.
Значит, выпуклость графика направлена вниз на всей области определения.
5. График функции изображен на рис. 2.
4

Рис. 2. График функции f(x) = 4x-1
Задания для самостоятельной работы
Исследовать функции и построить их графики:
1  ;
;
2.  ;
;
3.  ;
;
4.  .
.
 2020-01-14
2020-01-14 226
226








