Тема: «Вычисление площадей с помощью интегралов»
Цели урока:
Образовательные:
• знать общую схему и особенности вычисления площадей с помощью
интегралов;
• уметь проводить формализацию задачи.
Воспитательная:
• воспитание трудолюбия.
Развивающие:
• развитие познавательного интереса;
• развитие самостоятельности при работе с методическим материалом;
• формирование информационной культуры.
Методы обучения:
1. Проверочная работа;
2. Практическая работа.
План урока:
1. Организационный момент (3 мин)
2. Объявление целей урока (3 мин)
3. Практическая работа (30 мин)
4. Самостоятельная работа (40 мин)
5. Подведение итогов (4 мин)
Ход урока отображен в табл. 8.
Таблица 8.
Ход урока
| Учитель | Ученики | Тетрадь | ||||
| Здравствуйте. Садитесь. | Здравствуйте. |
| ||||
| Тема нашего сегодняшнего урока «Вычисление площадей с помощью интегралов». | Вычисление площадей с помощью интегралов | |||||
| Первый урок будет посвящен разбору примеров, после чего на втором уроке вы будете самостоятельно вычислять площади с помощью интегралов. |
| |||||
| Сейчас я вам выдам раздаточный материал, в котором подробно описан ход вычисления площадей. Внимательно изучите и поэтапно выполните то, что от вас требуется. Если кто-то выполняет задание раньше, он может приступать к задачам для самостоятельного решения, которые приведены в конце раздаточного материала. | Ученики берут раздаточный материал, садятся за компьюте-ры и начинают работать. | Задача 1. Найти площадь фигуры, ограниченной параболами у = х2, у = 2х-х2 и осью Ох. Построим графики функций у - х2, у = 2х - х2 и найдем абсциссы точек пересечения этих графиков из уравнения х2 = 2х - х2. Корни этого уравнения х1 = 0, х2 = 1. Данная фигура изображена на рис. 2.2. Из рисунка видно, что фигура состоит из двух криволинейных трапеций. Следовательно, искомая площадь равна сумме площадей этих трапеций: S =
Задача 2. Найти площадь S фигуры, ограниченной отрезком функции у = cos x на этом отрезке. Заметим, что площадь данной фигуры равна площади фигуры, симметричной данной относительно оси Ох, изображенной на рис. 2.3, т.е. площади фигуры, ограниченной отрезком | ||||

|
| Таблица | 8 (продолжение) | |||
| Учитель | Ученики | Тетрадь | ||||
|
| функции y = - cosx на отрезке
- cosx S = В общем, если f(x) площадь S криволинейной трапеции равна S = Задача 3. Найти площадь S фигуры, ограниченной параболой у = х2 +1 и прямой у = х + 3 Построим графики функций у = х2+1 и у = х + 3. Найдем абсциссы точек пересечения этих графиков из уравнения х2 +1= х+3. Это уравнение имеет корни x1 = -1, х2 = 2. Фигура, ограниченная графиками данных функций, изображена на рис. 2.4. Из этого рисунка видно, что искомую площадь можно найти как разность площадей S1 и S2 двух трапеций, опирающихся на отрезок [-1;2], первая из которых ограничена сверху отрезком прямой у = x + 3, а вторая - дугой параболы у = х2 + 1. Так как S1 = S = S1 – S2 =
Используя свойство первообразных, можно записать S в виде одного интеграла: S=
В общем, площадь фигуры равна: S = Эта формула справедлива для любых непрерывных функций f1(x) и f2 (х) (принимающих значения любых знаков), удовлетворяющих условию Задача 4. Найти площадь S фигуры, | |||||
 Таблица 8 (продолжение)
Таблица 8 (продолжение)
| Учитель | Ученики | Тетрадь |
| ограниченной параболами у = х2 и у = 2х2 -1. | ||
| Построим данную фигуру, которая изображена | ||
| на рис. 2.5, и найдем абсциссы точек пересечения | ||
| парабол из уравнения х2 = 2х2 -1. | ||
Это уравнение имеет корни x1,2= 
| ||
| Воспользуемся формулой (1). Здесь f1(x) = 2x2 -1, | ||
| f2(х) = х2. | ||
| S =
| ||
| Конец первого | ||
| урока. | Нет. |
|
| Все справились? | ||
| (Подходит к тем, | ||
| кто не успел и ищет | ||
| ошибку, указывает | ||
| на нее, но не | Да- | |
| исправляет.) | ||
| Все успели? | ||
| Начало второго | Делают | |
| урока. | самостоятельно. | |
| Переходим к | ||
| решению | ||
| самостоятельных | ||
| задач. | ||
| Внимательно | ||
| ознакомьтесь и | ||
| приступайте к | ||
| решению. Задания | ||
| выполняете в той | ||
| же форме, как и | ||
| примеры. При | ||
| затруднениях | ||
| поднимайте руку, я | ||
| подойду. | ||
| Итак, все успели? | Да. | |
| Сейчас я подойду к | ||
| каждому и проверю | ||
| решение. | ||
| У вас еще остались | ||
| вопросы по |
Таблица 8 (окончание)
| Учитель | Ученики | Тетрадь |
| пройденной теме? | ||
| Кто не успел решить | ||
| задачи на уроке, | ||
| должен будет их | ||
| доделать дома. |
Раздаточный материал (из учебника «Алгебра и начала анализа». Ш. А. Алимов,
Ю. М. Колягин, Ю. В. Сидоров и др.)-
Задача 1. Найти площадь фигуры, ограниченной параболами у = х2, у=2х-х2 и осью Ох.
Построим графики функций у = х2, у = 2х-х2 и найдем абсциссы точек
пересечения этих графиков из уравнения х2 =2х – х2. Корни этого уравнения х1= 0, х2 = 1. Данная фигура изображена на рис. 3
|
|
Рис. 3. Фигура, ограниченная параболами у = х2, у = 2х — х2 и осью Ох
Из рисунка видно, что фигура состоит из двух криволинейных трапеций. Следовательно, искомая площадь равна сумме площадей этих трапеций
S = 
Задача 2. Найти площадь S фигуры, ограниченной отрезком  оси Ох и графиком функции у = cos x на этом отрезке.
оси Ох и графиком функции у = cos x на этом отрезке.
Заметим, что площадь данной фигуры равна площади фигуры, симметричной данной относительно оси Ох, изображенной на рис. 4,
|
|
| y=cosx |
Рис. 4 Фигура, ограниченная отрезком  и графиком функции у= cosx
и графиком функции у= cosx
т.е. площади фигуры, ограниченной отрезком  оси Ох и графиком
оси Ох и графиком
функции y = -cosx на отрезке  . На этом отрезке – cos x > 0, и поэтому
. На этом отрезке – cos x > 0, и поэтому
S = 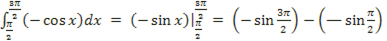 = 2
= 2
В общем, если f(x)<0 на отрезке [a;b], то площадь S криволинейной
трапеции равна S =  )dx
)dx
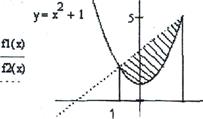
Задача 3. Найти площадь S фигуры, ограниченной параболой у = х2 +1 и прямой у = х + 3.
Построим графики функций у = х2 +1 и у = х + 3. Найдем абсциссы точек
пересечения этих графиков из уравнения х2+1=x+3. Это уравнение имеет корни х1 = -1, х2 = 2. Фигура, ограниченная графиками данных функций, изображена на рис. 5.
|
|
Рис. 5. Фигура, ограниченная параболой у =. x 2 +1 и прямой у = х + 3
Из этого рисунка видно, что искомую площадь можно найти как разность площадей S1 и S2 двух трапеций, опирающихся на отрезок [-1;2], первая из которых ограничена сверху отрезком прямой у = х+3, а вторая - дугой
параболы у = х2 + 1. Так как S1 = 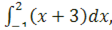 S2 =
S2 =  то
то
S = S1 – S2 = 
Используя свойство первообразных, можно записать S в виде одного интеграла:
S = 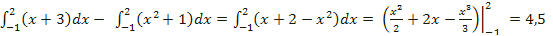
В общем, площадь фигуры равна:
S = 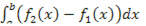
Эта формула справедлива для любых непрерывных функций f1(x) и f2(x) (принимающих значения любых знаков), удовлетворяющих условию
f2(x)  f1(x)
f1(x)
Задача 4. Найти площадь S фигуры, ограниченной параболами у = х2 и у = 2х2- 1
Построим данную фигуру, которая изображена на рис.6, и найдем абсциссы точек пересечения парабол из уравнения х2 = 2х2 -1.
 ОД
ОД
ОД
у = 2х - 1
Рис 6. Фигура, ограниченная параболами у = х2 и у = 2х2 -1
Это уравнение имеет корни x1,2 = ±1. Воспользуемся формулой (1). Здесь
| f1(x) = 2x2 -1, f2(х) = х2. | |
| S =
| |
Задания для самостоятельной работы.
Найти площадь фигуры, ограниченной:
1. Параболой у = 4х - х2, прямой у = 4 - х и осью Ох.
2. Параболой у = 3х2, прямой y = 1,5х + 4,5 и осью Ох.
3. Графиками функций у = 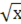 , у = (х-2)2 и осью Ох.
, у = (х-2)2 и осью Ох.
4. Графиками функций у = х3, у =2 х – х2 и осью Ох.
5. Графиком функции y = sin x, отрезком [0;π] оси Ох и прямой,
проходящей через точки (0;0) и 
6. Графиками функций у = sinx, у = cos x и отрезком  оси.
оси.
Приложение 2. Типологии познавательной активности учащихся.
Таблица 9.
| Методический подход (по Г. И. Щукиной) | Технологический подход (по Т. И. Шамовой) | Уровни интенсивности познавательной активности учащихся (уровневый подход) (по Е. В. Коротаевой) |
| Нулевая активность Учащийся пассивен, слабо реагирует на требования учителя, не проявляет желания к самостоятельной работе, предпочитает режим давления со стороны педагога. | ||
| Репродуктивно-подражательная активность Опыт в учебной деятельности накапливается через усвоение образцов, при этом уровень собственной активности личности недостаточен. | Воспроизводящая активность Ученик должен запомнить и воспроизвести полученные знания, овладеть способами применения знаний по образцу. | Относительная активность Активность учащихся проявляется лишь в определенных учебных ситуациях (зависит от интересного содержания урока, необычных приемов преподавания и т. д.), определяется в основном эмоциональным восприятием. |
| Поисково-исполнительская активность Ученик не просто принимает задачу, но и сам отыскивает средства ее выполнения (имеет место большая степень самостоятельности). | Интерпретирующая активность Выявление смысла, проникновение в сущность явления, стремление познать связи между явлениями, овладеть способом применения знаний в новых условиях. | Привычно-исполнительская активность Позиция учащихся обусловлена не только эмоциональной готовностью, но и наработанными привычными приемами учебных действий, что обеспечивает быстрое восприятие учебной задачи и самостоятельность в ходе ее решения. |
| Творческая активность Сама задача может ставиться школьником, и пути ее решения избираются новые, нестандартные. | Творческая активность Не просто проникновение в сущность явлений, их взаимосвязи, а попытка найти для этой цели новый способ. | Творческая активность Позиция учащихся характеризуется готовностью включаться в нестандартную учебную ситуацию, поиском новых средств для ее решения |
Познавательная активность.
Цель: выявление уровней познавательной активности учащихся 5 А класса на начало учебного года по методикеЕ. В. Коротаевой.
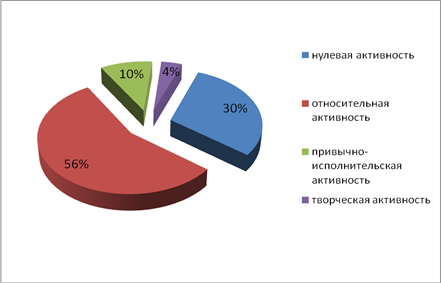
Цель: выявление уровней познавательной активности учащихся 5 А класса на конец первого полугодия по методикеЕ. В. Коротаевой.
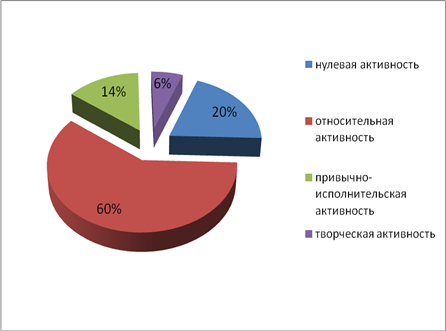
Цель: выявление уровней познавательной активности учащихся 10 Г класса на начало учебного года по методикеЕ. В. Коротаевой.
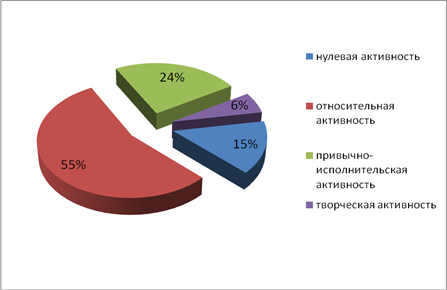
Цель: выявление уровней познавательной активности учащихся 10 Г класса на конец первого полугодия по методикеЕ. В. Коротаевой.
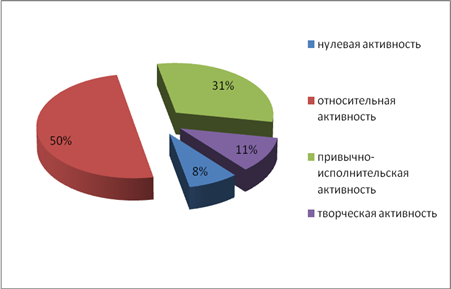
5 А класс

10 Г класс 
Данные были получены с помощью наблюдения, анализа учебной деятельности учащихся и различных методик тестирования.
 2020-01-14
2020-01-14 190
190
 = 1
= 1 оси Ох и графиком
оси Ох и графиком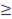 0, и поэтому
0, и поэтому = 2
= 2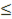 0 на отрезке [а; b], то
0 на отрезке [а; b], то
 S2 =
S2 =  то
то