Властивості соленоїдального поля

Як відомо, векторне поле 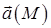, яке задовольняє в області  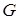умову 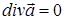, називається соленоїдальним в цій області. Нехай область  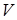є об’ємно однозв’язною. Це означає, що, якщо кусково-гладка замкнена поверхня  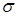лежить в області 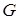, то і область, яка обмежує поверхню 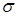, цілком належить області 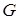. Прикладами об’ємно однозв’язних областей є куля, паралелепіпед, тор. Відзначимо, що тор не є поверхнево однозв’язною областю. Область, яка знаходиться між двома сферами, не є об’ємно однозв’язною (але є поверхнево однозв’язною).

Із формули Остроградського-Гаусса випливає, що соленоїдальне поле в взаємно однозв’язній області має таку властивість: потік соленоїдального поля через довільну замкнену поверхню, яка знаходиться в цій області, дорівнює нулю.

Відзначимо, що, якщо область не є об’ємно однозв’язною, то потік соленоїдального (в цій області) поля через замкнену поверхню, яка знаходиться в області, може бути відмінним від нуля. Так електричне поле 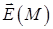 точкового заряду, який міститься в точці 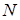, є соленоїдальним в кулі з викинутим центром ( 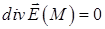при ).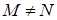

Слово «соленоїдальне» означає «трубасте». Для соленоїдального поля є справедливим закон збереження інтенсивності векторної трубки. З’ясуємо суть цього закону.

Нехай 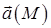 – соленоїдальне поле. Розглянемо відрізок «векторної трубки», тобто область, обмежену двома перерізами  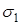і 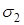 та боковою поверхнею 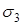, яка складається із векторних ліній (рис. 1). Застосуємо до такої області формулу Остроградського-Гаусса (8). Оскільки в соленоїдальному полі 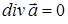, то потік векторного поля  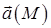через поверхню області дорівнює нулю:  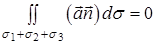( 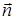– одиничний вектор зовнішньої нормалі). На боковій поверхні  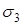маємо 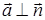, тому .

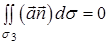Отже,

.

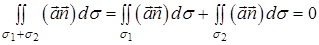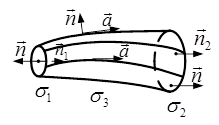
Рисунок 1 – Відрізок «векторної трубки»

Змінимо на перерізі 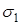 напрям нормалі  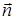на протилежний ( 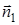– внутрішня нормаль до 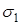). Тоді отримаємо

,

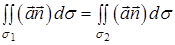де обидва потоки через перерізи 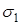 і 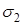 обчислюються в напрямі векторних ліній.

Таким чином, у соленоїдальному (трубчастому) векторному полі 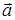 потік через будь-який переріз векторної трубки набуває одного й того самого значення. Це і є закон збереження інтенсивності збереження векторної трубки.