Потік векторного поля

Розглянемо векторне поле , визначене в просторовій області 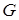, і деяку кусково-гладку орієнтовну поверхню . Нехай  – поле одиничних нормалей на обраній стороні поверхні .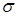

Як було відзначено в п. 4.2, поверхневий інтеграл

                                        (5)

називається потоком векторного поля  через поверхню  в сторону, яка визначається вектором  (кажуть також «потік через обрану сторону поверхні »).

Якщо взяти іншу сторону поверхні (змінити орієнтацію), то вектор  змінить напрям на протилежний; тому скалярний добуток , а отже, і потік (поверхневий інтеграл (5)) змінить знак.

Якщо  – швидкість рухомої рідини, то  є кількістю (об’ємом) рідини, яка протікає через поверхню 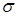 у напрямі нормалі  за одиницю часу. Ця величина називається у фізиці (гідродинаміці) потоком рідини через поверхню . Тому і у випадку довільного векторного поля  інтеграл (5) називається потоком векторного поля через поверхню .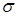

Розглянемо електричне поле  точкового заряду , який міститься в точці . Знайдемо потік векторного поля  через зовнішню сторону сфери  радіуса  з центром у точці . Нехай  ( – точка на сфері ); тоді . Тому

,

де  – діелектрична проникність середовища, .

Якщо в системі координат , а , то вираз (5) для потоку векторного поля  можна записати у вигляді

.     (6)

Кожен доданок у правій частині рівності (6) залежить від вибору системи координат, проте їх сума, тобто потік , очевидно, не залежить від вибору системи координат.