Властивості потенціального поля

Як відомо, векторне поле , яке задовольняє в області  умову , називається потенціальним у цій області ( – скалярний потенціал поля ). Якщо поле  потенціальне в області , то  і вираз  є повним диференціалом функції  в області . Це означає, що виконана умова незалежності криволінійного інтеграла від шляху інтегрування в просторі.

Таким чином, потенціальне в області  поле має такі властивості.

1. Циркуляція потенціального поля  вздовж довільного замкненого контуру  дорівнює нулю:

.

2. Для довільних точок  і  області  циркуляція потенціального поля  вздовж кривої  не залежить від вибору кривої  і дорівнює різниці значень потенціала  в точках  і :

.

У випадку силового потенціального поля ця властивість означає, що робота такого поля вздовж кривої  не залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок  і .

3. Потенціальне поле  є безвихровим, тобто .

Нехай тепер дано векторне поле , яке задовольняє в області  умову . Чи випливає звідси, що поле  є потенціальним в області ? Відповідь на це запитання залежить від форми області . Якщо область  є поверхнево однозв’язною, то із умови  випливає, що існує функція  така, що

.

Отже, , тобто поле  є потенціальним в області .

Таким чином, умова  є необхідною і достатньою умовою потенціальності поля  у поверхнево однозв’язній області.

Потенціал  потенціального поля  у поверхнево однозв’язній області можна обчислити за формулою:

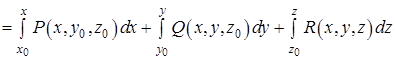.     (14)

Якщо область  не є поверхнево однозв’язною, то умова  не є достатньою для потенціальності поля  в області .